题目内容
已知向量
，
，且
，则m等于( )
| A．2 | B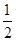． | C． | D． |
A
解析试题分析：因为，向量，，且，所以，·=-2+m=0,m=2,故选A。
考点：本题主要考查平面向量的坐标运算，向量垂直的条件。
点评：简单题，两向量垂直，两向量的数量积为0.
练习册系列答案
相关题目
平面四边形ABCD中
，则四边形ABCD是
| A．矩形 | B．正方形 | C．菱形 | D．梯形 |
已知向量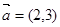
，
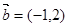，若
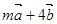与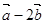
共线，则 ( )
A． | B． | C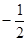． | D． |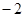
已知向量
,若
,则实数
的取值范围是( )
A． | B． |
C． | D． |
平面向量的集合
到的映射
，其中
为常向量．若映射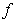
满足
对任意的
恒成立，则的坐标可能是（ ）
A．( ，) | B．(， ) | C．( ， ) | D．(，) |
在平行四边形ABCD中，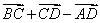
等于（ ）
A． | B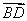． | C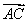． | D． |
已知向量
满足
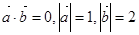，则
| A．0 | B．2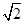 | C．4 | D．8 |
设为基底向量,已知向量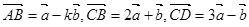
,若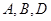
三点共线,则实数
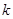的值等于
A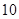． | B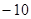． | C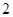． | D． |
已知向量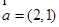
，
，且
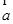与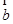
的夹角为锐角，则
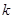的取值范围是（ ）
A． | B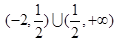． | C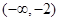． | D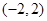． |