题目内容
已知函数f（x）=2cos2x+sin2x-4cosx。
（1）求f（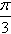
）的值；
（2）求f（x）的最大值和最小值。
（1）求f（
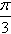）的值；（2）求f（x）的最大值和最小值。
解：（1）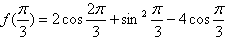
；
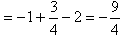（2）f（x）=2（2cos2x-1）+（1-cos2x）-4cosx =3cos2x-4cosx-1
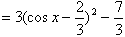（x∈R）
因为cosx∈[-1，1]，
所以，当cosx=-1时，f（x）取最大值6
当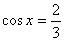
时，f（x）取最小值
。
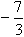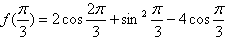
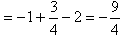；（2）f（x）=2（2cos2x-1）+（1-cos2x）-4cosx =3cos2x-4cosx-1
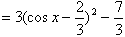（x∈R）因为cosx∈[-1，1]，
所以，当cosx=-1时，f（x）取最大值6
当
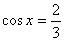时，f（x）取最小值。
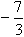练习册系列答案
阅读快车系列答案
相关题目