题目内容
 中,
中, ,顶点
,顶点 处分别有一枚半径为1的硬币(顶点
处分别有一枚半径为1的硬币(顶点 分别与硬币的中心重合)。向
分别与硬币的中心重合)。向 内部投一点,那么该点落在阴影部分的概率为
内部投一点,那么该点落在阴影部分的概率为
A. | B. | C. | D.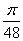 |
A
解析试题分析:根据题意, 中,
中, ,顶点
,顶点 处分别有一枚半径为1的硬币,那么可知那么利用扇形面积公式可知,三个扇形的面积为
处分别有一枚半径为1的硬币,那么可知那么利用扇形面积公式可知,三个扇形的面积为 ,三角形的面积为
,三角形的面积为 故可知阴影部分的面积为24-
故可知阴影部分的面积为24- ,则该点落在阴影部分的概率为
,则该点落在阴影部分的概率为 ,选A
,选A
考点:几何概型
点评:主要是求解扇形面积,然后利用三角形的面积减去扇形的面积即为阴影部分的面积,属于基础题。

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
右表是一个 列联表,则表中
列联表,则表中 处的值分别为
处的值分别为
| A.94 96 | B.52 50 |
| C.52 60 | D.54 52 |
某人射击一次击中的概率为0.6,经过3次射击,此人恰有两次击中目标的概率为( )
A. | B. | C. | D.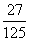 |
从装有2个黑球和2个白球的口袋内任取2个球,那么互斥而对立的两个事件是( )
| A.至少有1个黑球,至少有1个白球 | B.恰有1个黑球,恰有2个白球 |
| C.至少有1个黑球,都是黑球 | D.至少有1个黑球,都是白球 |
已知 .若在区域A中随机的扔一颗豆子,求该豆子落在区域B中的概率为
.若在区域A中随机的扔一颗豆子,求该豆子落在区域B中的概率为
A. | B. | C. | D. |
设随机变量 的分布列为
的分布列为 ,则
,则 ( )
( )
A. | B.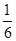 | C. | D. |
 (所以判断性别与运动有关,那么这种判断出错的可能性为( )(注:
(所以判断性别与运动有关,那么这种判断出错的可能性为( )(注: )
)










