题目内容
已知函数f(x)=2+log3x,x∈[1,9],则函数y=[f(x)]2+f(x2)的值域为_ .
【答案】分析:先求出函数y=[f(x)]2+f(x2)的定义域,然后将函数化成关于log3x的二次函数,进行配方找出对称轴,而0≤log3x≤1,利用对称轴与区间的位置关系求出最值,即可求出值域.
解答:解:∵f(x)=2+log3x,x∈[1,9],
∴y=[f(x)]2+f(x2)的定义域为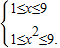
解得1≤x≤3,即定义域为[1,3].
∴0≤log3x≤1.
又y=[f(x)]2+f(x2)
=(2+log3x)2+2+log3x2
=(log3x)2+6log3x+6
=(log3x+3)2-3,
∵0≤log3x≤1,
∴6≤y≤13.
故函数的值域为[6,13].
故答案为:[6,13]
点评:本题以对数函数为载体考查二次函数的值域,属于求二次函数的最值问题,解题的关键是定义域,属于基本题.
解答:解:∵f(x)=2+log3x,x∈[1,9],
∴y=[f(x)]2+f(x2)的定义域为
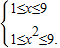
解得1≤x≤3,即定义域为[1,3].
∴0≤log3x≤1.
又y=[f(x)]2+f(x2)
=(2+log3x)2+2+log3x2
=(log3x)2+6log3x+6
=(log3x+3)2-3,
∵0≤log3x≤1,
∴6≤y≤13.
故函数的值域为[6,13].
故答案为:[6,13]
点评:本题以对数函数为载体考查二次函数的值域,属于求二次函数的最值问题,解题的关键是定义域,属于基本题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目