题目内容
(本小题满分14分)(注意:在试题卷上作答无效)
设数列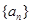 的前
的前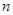 项和为
项和为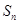 ,对一切
,对一切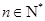 ,点
,点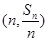 都在函数
都在函数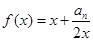 的图象上.
的图象上.
(Ⅰ)求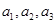 及数列
及数列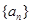 的通项公式
的通项公式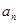 ;
;
(Ⅱ) 将数列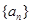 依次按1项、2项、3项、4项循环地分为(
依次按1项、2项、3项、4项循环地分为(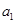 ),(
),( ,
,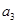 ),(
),(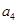 ,
,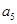 ,
,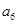 ),(
),(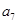 ,
,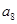 ,
,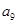 ,
, );(
);(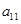 ),(
),(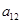 ,
,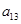 ),(
),(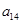 ,
,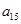 ,
,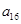 ),(
),(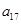 ,
,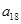 ,
,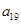 ,
,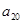 );(
);(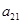 ),…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为
),…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为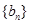 ,求
,求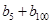 的值;
的值;
(Ⅲ)令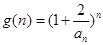 (
( ),求证:
),求证: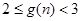
(Ⅰ)  ,
, ,
, ,
,
(Ⅱ)  =2010
=2010
(Ⅲ)
【解析】解:(1)因为点 在函数
在函数 的图象上,
的图象上,
故 ,所以
,所以 .令
.令 ,得
,得 ,所以
,所以 ;
;
令 ,得
,得 ,
,
 ;令
;令 ,得
,得 ,
, .
.
由此猜想: .
.
用数学归纳法证明如下:
① 当 时,有上面的求解知,猜想成立.
时,有上面的求解知,猜想成立.
② 假设 时猜想成立,即
时猜想成立,即 成立,
成立,
则当 时,注意到
时,注意到
 ,
,
故 ,
, .
.
两式相减,得 ,所以
,所以 .
.
由归纳假设得, ,故
,故 .
.
这说明 时,猜想也成立.
时,猜想也成立.
由①②知,对一切 ,
, 成立
. …………………………………………4分
成立
. …………………………………………4分
另解:因为点 在函数
在函数 的图象上,
的图象上,
故 ,所以
,所以 ①.令
①.令 ,得
,得 ,所以
,所以 ;
;
 时
时 ②
②
 时①-②得
时①-②得
令 ,
,
即 与
与 比较可得
比较可得
 ,解得
,解得 .
.
因此
又 ,所以
,所以 ,从而
,从而 .
…………4分
.
…………4分
(2)因为 (
( ),所以数列
),所以数列 依次按1项、2项、3项、4项循环地分为(2),(4,6),(8,10,12),(14,16,18,20);(22),(24,26),(28,30,32),(34,36,38,40);(42),…. 每一次循环记为一组.由于每一个循环含有4个括号, 故
依次按1项、2项、3项、4项循环地分为(2),(4,6),(8,10,12),(14,16,18,20);(22),(24,26),(28,30,32),(34,36,38,40);(42),…. 每一次循环记为一组.由于每一个循环含有4个括号, 故  是第25组中第4个括号内各数之和.由分组规律知,由各组第4个括号中所有第1个数组成的数列是等差数列,且公差为20. 同理,由各组第4个括号中所有第2个数、所有第3个数、所有第4个数分别组成的数列也都是等差数列,且公差均为20. 故各组第4个括号中各数之和构成等差数列,且公差为80. 注意到第一组中第4个括号内各数之和是68,
是第25组中第4个括号内各数之和.由分组规律知,由各组第4个括号中所有第1个数组成的数列是等差数列,且公差为20. 同理,由各组第4个括号中所有第2个数、所有第3个数、所有第4个数分别组成的数列也都是等差数列,且公差均为20. 故各组第4个括号中各数之和构成等差数列,且公差为80. 注意到第一组中第4个括号内各数之和是68,
所以  .又
.又 =22,所以
=22,所以 =2010. ………………9分
=2010. ………………9分
(3)有(1)中知 ,∴
,∴ ,
,
当 时,
时, ;
;
当 时,
时,
显然
而 (
( )
)

 。…………………14分
。…………………14分

 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)