题目内容
给出下列四个命题,其中正确的命题有①函数y=2sin(2x-
| π |
| 3 |
| 5π |
| 12 |
②函数f(x)=4sin(2x+
| π |
| 3 |
| π |
| 6 |
③若f(sinx)=cos6x,则f(cos15°)=0;
④正弦函数在第一象限为增函数.
分析:①函数y=2sin(2x-
)有一条对称轴方程是x=
,由正弦函数的性质直接求出对称轴方程比较即可;
②函数f(x)=4sin(2x+
)(x∈R),可改写成y=4cos(2x+
),由图象变换的规则进行判断;
③若f(sinx)=cos6x,则f(cos15°)=0,利用所给的函数的解析式的运算规则直接求值;
④正弦函数在第一象限为增函数,由正弦函数的性质进行判断.
| π |
| 3 |
| 5π |
| 12 |
②函数f(x)=4sin(2x+
| π |
| 3 |
| π |
| 6 |
③若f(sinx)=cos6x,则f(cos15°)=0,利用所给的函数的解析式的运算规则直接求值;
④正弦函数在第一象限为增函数,由正弦函数的性质进行判断.
解答:解:①函数y=2sin(2x-
)有一条对称轴方程是x=
是正确命题,令2x-
=kπ+
,解得x=
+
,当k=0时既得;
②函数f(x)=4sin(2x+
)(x∈R),可改写成y=4cos(2x+
)是错误命题,因为f(x)=4sin(2x+
)=-4cos(2x+
)(x∈R)≠y=4cos(2x+
);
③若f(sinx)=cos6x,则f(cos15°)=0,因为cos15°=sin75°,故f(cos15°)=;
④正弦函数在第一象限为增函数是错误命题,由函数的周期性可知.
故答案为①③
| π |
| 3 |
| 5π |
| 12 |
| π |
| 3 |
| π |
| 2 |
| 5π |
| 12 |
| kπ |
| 2 |
②函数f(x)=4sin(2x+
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| 5π |
| 6 |
| π |
| 6 |
③若f(sinx)=cos6x,则f(cos15°)=0,因为cos15°=sin75°,故f(cos15°)=;
④正弦函数在第一象限为增函数是错误命题,由函数的周期性可知.
故答案为①③
点评:本题考查命题真假的判断与应用,求解本题的关键是对命题中涉及的正弦函数的对称性、三角函数的图象变换等基础知识熟练掌握的程度,能否灵活运用.本题中④很有迷惑性,是一个易错点,解题时要注意.

练习册系列答案
相关题目


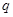 是等比数列
是等比数列 的公比,则“数列
的公比,则“数列 ”的既不充分也不必要条件;
”的既不充分也不必要条件; 上的函数
上的函数 是奇函数,则对定义域内的任意
是奇函数,则对定义域内的任意 必有
必有 ;
; 满足
满足 ,则
,则 的一个正周期为
的一个正周期为 ;
; 与
与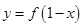 图像关于
图像关于 对称.
对称.