题目内容
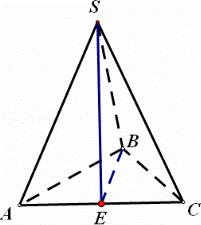
在三棱锥S﹣ABC中SA=SC=AB=BC，则直线SB与AC所成角的大小为 ．
解答：
解：取AC中点E，连接SE，BE
∵SA=SC
∴SE⊥AC
同理得：BE⊥AC
∵SE∩BE=E，SE，BE⊂面SBE
∴AE⊥面SBE
∵SB⊂面SBE
∴AE⊥SB
即：直线SB与AC所成角为90°
故答案为：90°
点评：
本题考查的知识点是空间异面直线及其所成的角，解答的关键是熟练掌握空间线线垂直与线面垂直之间的相互转化．
练习册系列答案
名校课堂系列答案
相关题目
在三棱锥S-ABC中，∠ASB=∠ASC=∠BSC=60°，则侧棱SA与侧面SBC所成的角的大小是
如图，在三棱锥S-ABC中，BC⊥平面SAC，AD⊥SC．
在三棱锥S-ABC中，∠SAB=∠SAC=∠ACB=90°，且AC=BC=5，SB=5
（2011•许昌一模）在三棱锥S-ABC中，△ABC是边长为4的正三角形，平面SAC⊥平面ABC，SA=SC=