题目内容

(本题满分8分)求下列曲线的的标准方程:

(1) 离心率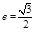且椭圆经过.

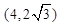(2) 渐近线方程是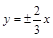，经过点.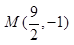

【答案】

(1)

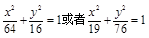
(2)

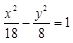
【解析】解:（1）由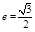可得b=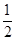a,因此设椭圆方程为(1),

将点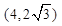的坐标代入可得(1)b²=16,(2)b²=19,

所求方程是: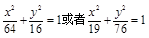.--------4分

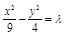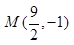（2）设所求双曲线方程是,将代入可得,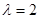

所以,所求双曲线方程是: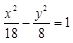.-----------8分

练习册系列答案

轻松课堂标准练系列答案

（本题满分8分．老教材试题第1小题4分，第2小题4分；新教材试题第1小题3分，第2小题5分．）
（老教材）
设a为实数，方程2x²-8x+a+1=0的一个虚根的模是 $数学公式$ ．
（1）求a的值；
（2）在复数范围内求方程的解．（新教材）
设函数f（x）=2^x+p，（p为常数且p∈R）
（1）若f（3）=5，求f（x）的解析式；
（2）在满足（1）的条件下，解方程：f^-1（x）=2+log₂x²．

（本题满分14分）

某运动员进行20次射击练习，记录了他射击的有关数据，得到下表：

环数	7	8	9	10
命中次数	2	7	8	3

（Ⅰ）求此运动员射击的环数的平均数；

（Ⅱ）若将表中某一环数所对应的命中次数作为一个结果，在四个结果（2次、7次、8次、3次）中，随机取2个不同的结果作为基本事件进行研究，记这两个结果分别为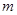次、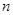次，每个基本事件为（m，n）.求“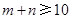”的概率.

（本题满分8分）已知函数.

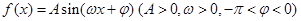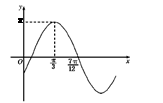
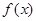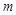
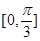(1)若的部分图象如图所示，求的解析式;

(2)在(1)的条件下，求最小正实数，使得函数的图象向左平移个单位后所对应的函数是偶函数;

(3)若在上是单调递增函数，求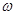的最大值.

试题分类