题目内容
已知函数f(x)=ax+lnx,x∈(1,e),且f(x)有极值.
(I)求实数a的取值范围;
(Ⅱ)若l<m<n<e,证明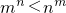 ;
;
(Ⅲ)函数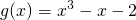 ,证明:?x1∈(1,e),?x0∈(1,e),使得g(x0)=f(x1)成立.
,证明:?x1∈(1,e),?x0∈(1,e),使得g(x0)=f(x1)成立.
(I)解:由f(x)=ax+lnx求导可得:f′(x)=a+ .
.
令f′(x)=a+ =0,可得a=-
=0,可得a=-
∵x∈(1,e),∴- ∈(-1,-
∈(-1,- ),∴a∈(-1,-
),∴a∈(-1,- )
)
又x∈(1,e)时
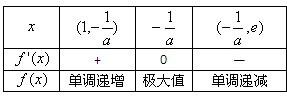
∴f(x)有极值时实数a的取值范围为(-1,- );
);
(Ⅱ)要证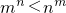 ,即证nlnm<mlnn,即证
,即证nlnm<mlnn,即证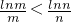
令F(x)= ,x∈(1,e),则F′(x)=
,x∈(1,e),则F′(x)=
∴当x∈(1,e)时,F′(x)>0,∴F(x)在(1,e)上为增函数
∵l<m<n<e,∴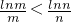 ,
,
∴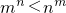 ;
;
(Ⅲ)证明:由g(x)=x3-x-2求导可得g'(x)=3x2-1
令g'(x)=3x2-1=0,解得x=±
令g'(x)=3x2-1>0,解得x<- 或x>
或x>
又∵x∈(1,e)⊆( ,+∞),∴g(x)在(1,e)上为单调递增函数
,+∞),∴g(x)在(1,e)上为单调递增函数
∵g(1)=-2,g(e)=e3-e-2,∴g(x)在x∈(1,e)的值域为(-2,e3-e-2)
∵e3-e-2>-1+ln(- ),-2<ae+1,-2<a
),-2<ae+1,-2<a
∴(ae+1,-1+ln(- )]⊆(-2,e3-e-2),
)]⊆(-2,e3-e-2),
(a,-1+ln(- )]⊆(-2,e3-e-2)
)]⊆(-2,e3-e-2)
∴?x1∈(1,e),?x0∈(1,e),使得g(x0)=f(x1)成立.
分析:(I)由f(x)=ax+lnx求导,再由f(x)有极值知f′(x)=0解,且在两侧导函数正负相异求解.
(Ⅱ)要证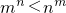 ,即证nlnm<mlnn,即证
,即证nlnm<mlnn,即证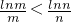 ,构造函数F(x)=
,构造函数F(x)= ,x∈(1,e),证明F(x)在(1,e)上为增函数,即可证得结论;
,x∈(1,e),证明F(x)在(1,e)上为增函数,即可证得结论;
(Ⅲ)由?x1∈(1,e),?x0∈(1,e),使得g(x0)=f(x1)f(x1)即研究:f(x)的值域是g(x)的值域的子集,所以分别求得两函数的值域即可.
点评:本题主要考查用导数来研究函数的单调性,极值,最值等问题,考查不等式的证明,属于中档题.
 .
.令f′(x)=a+
 =0,可得a=-
=0,可得a=-
∵x∈(1,e),∴-
 ∈(-1,-
∈(-1,- ),∴a∈(-1,-
),∴a∈(-1,- )
)又x∈(1,e)时

∴f(x)有极值时实数a的取值范围为(-1,-
 );
);(Ⅱ)要证
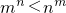 ,即证nlnm<mlnn,即证
,即证nlnm<mlnn,即证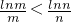
令F(x)=
 ,x∈(1,e),则F′(x)=
,x∈(1,e),则F′(x)=
∴当x∈(1,e)时,F′(x)>0,∴F(x)在(1,e)上为增函数
∵l<m<n<e,∴
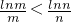 ,
,∴
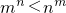 ;
;(Ⅲ)证明:由g(x)=x3-x-2求导可得g'(x)=3x2-1
令g'(x)=3x2-1=0,解得x=±

令g'(x)=3x2-1>0,解得x<-
 或x>
或x>
又∵x∈(1,e)⊆(
 ,+∞),∴g(x)在(1,e)上为单调递增函数
,+∞),∴g(x)在(1,e)上为单调递增函数∵g(1)=-2,g(e)=e3-e-2,∴g(x)在x∈(1,e)的值域为(-2,e3-e-2)
∵e3-e-2>-1+ln(-
 ),-2<ae+1,-2<a
),-2<ae+1,-2<a∴(ae+1,-1+ln(-
 )]⊆(-2,e3-e-2),
)]⊆(-2,e3-e-2),(a,-1+ln(-
 )]⊆(-2,e3-e-2)
)]⊆(-2,e3-e-2)∴?x1∈(1,e),?x0∈(1,e),使得g(x0)=f(x1)成立.
分析:(I)由f(x)=ax+lnx求导,再由f(x)有极值知f′(x)=0解,且在两侧导函数正负相异求解.
(Ⅱ)要证
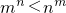 ,即证nlnm<mlnn,即证
,即证nlnm<mlnn,即证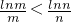 ,构造函数F(x)=
,构造函数F(x)= ,x∈(1,e),证明F(x)在(1,e)上为增函数,即可证得结论;
,x∈(1,e),证明F(x)在(1,e)上为增函数,即可证得结论;(Ⅲ)由?x1∈(1,e),?x0∈(1,e),使得g(x0)=f(x1)f(x1)即研究:f(x)的值域是g(x)的值域的子集,所以分别求得两函数的值域即可.
点评:本题主要考查用导数来研究函数的单调性,极值,最值等问题,考查不等式的证明,属于中档题.

练习册系列答案
相关题目