题目内容
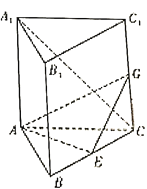
【题目】在五面体![]() 中,
中, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() .
.
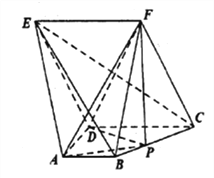
(1) 证明: 直线![]() 平面
平面![]() ;
;
(2) 已知![]() 为棱
为棱![]() 上的点,试确定
上的点,试确定![]() 点位置,使二面角
点位置,使二面角![]() 的大小为
的大小为![]() .
.
【答案】(1)见解析;(2) ![]() 点靠近
点靠近![]() 点的
点的![]() 的三等分点处.
的三等分点处.
【解析】试题分析:(1)证明一条直线垂直一个平面,只需要证明这条两个平面垂直,直线垂直两个平面的交线即可.证明CE⊥DF。∵平面CDEF⊥平面ABCD,平面CDEF∩平面ABCD=CD,CE⊥AD,即可得到直线CE⊥平面ADF.(2)根据题意,取EF的中点G,证明DA,DC,DG两两垂直.以D为原点,DA,DC,DG的方向为x,y,z轴,建立空间直角坐标系,进行计算,确定P在棱BC上的位置.
(1)∵![]() , ∴
, ∴![]()
∴四边形![]() 为菱形,∴
为菱形,∴![]()
∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
∵![]() ∴
∴![]() 平面
平面![]()
∴![]() ,又∵
,又∵![]()
∴直线![]() 平面
平面![]()
(2)∵![]() ,
,
∴![]() 为正三角形,取
为正三角形,取![]() 的中点
的中点![]() ,连接
,连接![]() ,则
,则![]()
∴![]() ,
,
∵平面![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]()
∵![]() ∴
∴![]() 两两垂直
两两垂直
以![]() 为原点,
为原点, ![]() 的方向为
的方向为![]() 轴,
轴,
建立空间直角坐标系
∵![]() ,
, ![]() ,
,
∴![]()
由(1)知![]() 是平面
是平面![]() 的法向量
的法向量
∵![]() ,
,![]()
设![]() ,
,
则![]() .
.
设平面![]() 的法向量为
的法向量为![]()
∵![]() , ∴
, ∴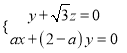 ,
,
令![]() ,则
,则![]()
∴![]()
∵二面角![]() 为
为![]() ,
,
∴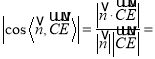
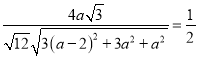 ,解得
,解得![]()
∴![]() 点靠近
点靠近![]() 点的
点的![]() 的三等分点处
的三等分点处

练习册系列答案
相关题目