题目内容
(2006•广州一模)在长方体ABCD-A1B1C1D1中,AB=4,AD=5,AA1=3,则四棱锥B1-A1BCD1的体积是( )
分析:以DA为x轴,以DC为y轴,以DD1为z轴,建立空间直角坐标系,由长方体ABCD-A1B1C1D1中,AB=4,AD=5,AA1=3,知
=(-5,0,0),
=(0,4,-3),故平面A1BCD1的法向量为
=(x,y,z),所以点B1到平面A1BCD1的距离d=
=
,S四边形A1BCD1=5×5=25,由此能求出四棱锥B1-A1BCD1的体积.
| A1D1 |
| A1B |
| n |
| |0+12+0| | ||
|
| 12 |
| 5 |
解答: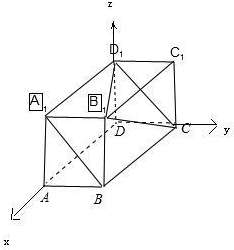 解:以DA为x轴,以DC为y轴,以DD1为z轴,建立空间直角坐标系,
解:以DA为x轴,以DC为y轴,以DD1为z轴,建立空间直角坐标系,
∵长方体ABCD-A1B1C1D1中,AB=4,AD=5,AA1=3,
∴A1(5,0,3),B(5,4,0),D1(0,0,3),B1(5,4,3),
∴
=(-5,0,0),
=(0,4,-3),
设平面A1BCD1的法向量为
=(x,y,z),
则
,∴
=(0,3,4),
∵
=(0,4,0),
∴点B1到平面A1BCD1的距离d=
=
,
长方体ABCD-A1B1C1D1中,AB=4,AD=5,AA1=3,
∴A1B=
=
=5,
∴S四边形A1BCD1=A1D1×A1B=5×5=25,
∴四棱锥B1-A1BCD1的体积V四棱锥B1-A1BCD1=
×S四边形A1BCD1×
=
×25×
=20.
故选B.
 解:以DA为x轴,以DC为y轴,以DD1为z轴,建立空间直角坐标系,
解:以DA为x轴,以DC为y轴,以DD1为z轴,建立空间直角坐标系,∵长方体ABCD-A1B1C1D1中,AB=4,AD=5,AA1=3,
∴A1(5,0,3),B(5,4,0),D1(0,0,3),B1(5,4,3),
∴
| A1D1 |
| A1B |
设平面A1BCD1的法向量为
| n |
则
|
| n |
∵
| A1B1 |
∴点B1到平面A1BCD1的距离d=
| |0+12+0| | ||
|
| 12 |
| 5 |
长方体ABCD-A1B1C1D1中,AB=4,AD=5,AA1=3,
∴A1B=
| AA12+AB2 |
| 9+16 |
∴S四边形A1BCD1=A1D1×A1B=5×5=25,
∴四棱锥B1-A1BCD1的体积V四棱锥B1-A1BCD1=
| 1 |
| 3 |
| 12 |
| 5 |
| 1 |
| 3 |
| 12 |
| 5 |
故选B.
点评:本题考查棱锥的体积的求法,是基础题.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
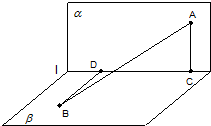 (2006•广州一模)如图,长度为2的线段AB夹在直二面角α-l-β的两个半平面内,A∈α,B∈β,
(2006•广州一模)如图,长度为2的线段AB夹在直二面角α-l-β的两个半平面内,A∈α,B∈β,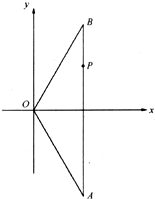 (2006•广州一模)如下图,在△OAB中,|OA|=|OB|=4,点P分线段AB所成的比为3:1,以OA、OB所在直线为渐近线的双曲线M恰好经过点P,且离心率为2.
(2006•广州一模)如下图,在△OAB中,|OA|=|OB|=4,点P分线段AB所成的比为3:1,以OA、OB所在直线为渐近线的双曲线M恰好经过点P,且离心率为2.