题目内容
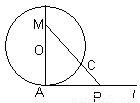
如图,已知圆心为O,半径为1的圆与直线l相切于点A,一动点P自切点A沿直线l向右移动时,取弧AC的长为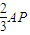 ,直线PC与直线AO交于点M.又知当AP=
,直线PC与直线AO交于点M.又知当AP=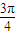 时,点P的速度为v,求这时点M的速度.
时,点P的速度为v,求这时点M的速度.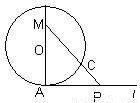
【答案】分析:设AP的长为x,AM的长为y,用x表示y,并用复合函数求导法则对时间t进行求导.
解答: 解:如图,作CD⊥AM,并设AP=x,AM=y,∠COA=θ,
解:如图,作CD⊥AM,并设AP=x,AM=y,∠COA=θ,
由题意弧AC的长为 ,半径OC=1,可知θ=
,半径OC=1,可知θ= ,考虑θ∈(0,π).
,考虑θ∈(0,π).
∵△APM∽△DCM,∴ .
.
∵DM=y-(1-cos ),DC=sin
),DC=sin ,∴
,∴
∴ .
.
上式两边对时间t进行求导,则y′t=y′x•x′t.
∴y′t=
当 时,x′t=v,代入上式得点M的速度
时,x′t=v,代入上式得点M的速度 .
.
点评:本题是难度较大题目,考查了弦长、弧度、相似、特别是复合函数的导数,以及导数的几何意义;
同时也考查了逻辑思维能力和计算能力.
解答:
 解:如图,作CD⊥AM,并设AP=x,AM=y,∠COA=θ,
解:如图,作CD⊥AM,并设AP=x,AM=y,∠COA=θ,由题意弧AC的长为
 ,半径OC=1,可知θ=
,半径OC=1,可知θ= ,考虑θ∈(0,π).
,考虑θ∈(0,π).∵△APM∽△DCM,∴
 .
.∵DM=y-(1-cos
 ),DC=sin
),DC=sin ,∴
,∴
∴
 .
.上式两边对时间t进行求导,则y′t=y′x•x′t.
∴y′t=

当
 时,x′t=v,代入上式得点M的速度
时,x′t=v,代入上式得点M的速度 .
.点评:本题是难度较大题目,考查了弦长、弧度、相似、特别是复合函数的导数,以及导数的几何意义;
同时也考查了逻辑思维能力和计算能力.

练习册系列答案
相关题目
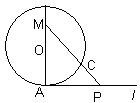 如图,已知圆心为O,半径为1的圆与直线l相切于点A,一动点P自切点A沿直线l向右移动时,取弧AC的长为
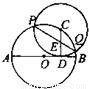
如图,已知圆心为O,半径为1的圆与直线l相切于点A,一动点P自切点A沿直线l向右移动时,取弧AC的长为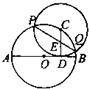 11、如图,已知AB为⊙O的直径,C为⊙O上一点,CD⊥AB于D,AD=9,BD=4,以C为圆心,CD为半径的圆与⊙O相交于P,Q两点,弦PQ交CD于E,则PE•EQ的值是
11、如图,已知AB为⊙O的直径,C为⊙O上一点,CD⊥AB于D,AD=9,BD=4,以C为圆心,CD为半径的圆与⊙O相交于P,Q两点,弦PQ交CD于E,则PE•EQ的值是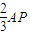 ,直线PC与直线AO交于点M.又知当AP=
,直线PC与直线AO交于点M.又知当AP= 时,点P的速度为v,求这时点M的速度.
时,点P的速度为v,求这时点M的速度.