题目内容
已知ω为正实数,函数f(x)=2sinωx在区间[-
,
]上递增,那么( )
| π |
| 3 |
| π |
| 4 |
A.0<ω≤
| B.0<ω≤2 | C.0<ω≤
| D.ω≥
|
∵sinx在[-
,
]是增函数
这里-
≤x≤
-
ω≤ωx≤
ω
所以有-
≤-
ω≤ωx≤
ω≤
∴-
≤-
ω∴ω≤
ω≤
∴ω≤2
所以0<ω≤
故选C.
| π |
| 2 |
| π |
| 2 |
这里-
| π |
| 3 |
| π |
| 4 |
-
| π |
| 3 |
| π |
| 4 |
所以有-
| π |
| 2 |
| π |
| 3 |
| π |
| 4 |
| π |
| 2 |
∴-
| π |
| 2 |
| π |
| 3 |
| 3 |
| 2 |
| π |
| 4 |
| π |
| 2 |
所以0<ω≤
| 3 |
| 2 |
故选C.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 、
、 为正实数,函数
为正实数,函数 在
在 上的最大值为
上的最大值为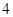 ,则
,则 在
在 上的最小值为
.
上的最小值为
. ,
, 为正实数,函数
为正实数,函数 在
在 上的最大值为
上的最大值为 ,则
,则 在
在 上的最小值为 .
上的最小值为 . (e为自然对数的底数).
(e为自然对数的底数).