题目内容
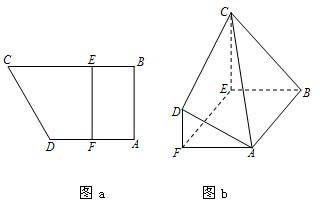
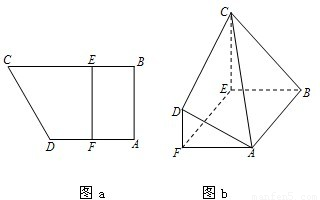
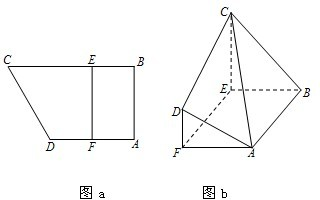 如图a所示,在直角梯形ABCD中,AB⊥AD,AD∥BC,F为AD的中点,E在BC上,且EF∥AB.已知AB=AD=CE=2,沿线段EF把四边形CDEF折起如图b所示,使平面CDEF⊥平面ABEF.
如图a所示,在直角梯形ABCD中,AB⊥AD,AD∥BC,F为AD的中点,E在BC上,且EF∥AB.已知AB=AD=CE=2,沿线段EF把四边形CDEF折起如图b所示,使平面CDEF⊥平面ABEF.(1)求证:AF⊥平面CDEF;
(2)求三棱锥C-ADE的体积;
(3)求二面角B-AC-D的余弦值.
分析:(1)由平面CDFE⊥平面ABEF,AF⊥FE,根据面面垂直的性质定理可得AF⊥平面CDEF;
(2)AF为三棱锥A-CDE的高,计算出AF的长及底面三角形ADE的面积,代入棱锥体积公式可得答案;
(3)利用二面角B-AC-D的余弦值为
,即可求得结论.
(2)AF为三棱锥A-CDE的高,计算出AF的长及底面三角形ADE的面积,代入棱锥体积公式可得答案;
(3)利用二面角B-AC-D的余弦值为
| S△ADC |
| S△ABC |
解答:(1)证明:∵平面CDFE⊥平面ABEF,且平面CDFE∩平面ABEF=EF,AF⊥FE,AF?平面ABEF,
∴AF⊥平面CDEF;
(2)解:由(1)知,AF为三棱锥A-CDE的高,且AF=1,
又∵AB=CE=2,∴S△CDE=
×2×2=2,
故三棱锥C-ADE体积V=
AF•S△CDE=
;
(3)解:由题意,AD=
,CD=
,BC=
,AB=2,AC=3
∴S△ABC=
AB•BC=
∵cos∠DCA=
=
=
∴sin∠DCA=
∴S△ADC=
DC•ACsin∠DCA=
•
•3•
=
∴二面角B-AC-D的余弦值为
=
=
.
∴AF⊥平面CDEF;
(2)解:由(1)知,AF为三棱锥A-CDE的高,且AF=1,
又∵AB=CE=2,∴S△CDE=
| 1 |
| 2 |
故三棱锥C-ADE体积V=
| 1 |
| 3 |
| 2 |
| 3 |
(3)解:由题意,AD=
| 2 |
| 5 |
| 5 |
∴S△ABC=
| 1 |
| 2 |
| 5 |
∵cos∠DCA=
| DC2+AC2-AD2 |
| 2DC•AC |
| 5+9-2 | ||
2
|
| 2 | ||
|
∴sin∠DCA=
| 1 | ||
|
∴S△ADC=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 1 | ||
|
| 3 |
| 2 |
∴二面角B-AC-D的余弦值为
| S△ADC |
| S△ABC |
| ||
|
3
| ||
| 10 |
点评:本题考查的知识点是直线与平面垂直的判定,棱锥的体积,考查面面角,解题的关键是熟练掌握面面垂直,线面垂直及线线垂直的相互转化,判断出棱锥的高和底面面积,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

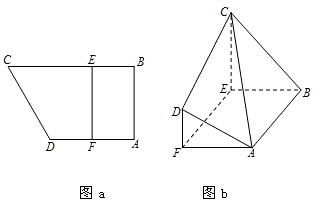 如图a所示,在直角梯形ABCD中,AB⊥AD,AD∥BC,F为AD的中点,E在BC上,且EF∥AB.已知AB=AD=CE=2,沿线段EF把四边形CDEF折起如图b所示,使平面CDEF⊥平面ABEF.
如图a所示,在直角梯形ABCD中,AB⊥AD,AD∥BC,F为AD的中点,E在BC上,且EF∥AB.已知AB=AD=CE=2,沿线段EF把四边形CDEF折起如图b所示,使平面CDEF⊥平面ABEF.