题目内容
若关于x的不等式mx2+2x+4＞0的解集为{x|-1＜x＜2}，则实数m的值为 ．
【答案】分析：由题意知，不等式mx2+2x+4＞0所对应的函数y=mx2+2x+4的开口向下，并且x=-1，与x=2是其对应方程mx2+2x+4=0的根，由韦达定理便可解得m的值．
解答：解：由题意知x=-1，与x=2是方程mx2+2x+4=0的两根，由韦达定理得：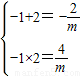
，解得m=-2．
点评：本题考查一元二次不等式的解法．
解答：解：由题意知x=-1，与x=2是方程mx2+2x+4=0的两根，由韦达定理得：
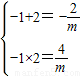，解得m=-2．点评：本题考查一元二次不等式的解法．
练习册系列答案
状元坊全程突破导练测系列答案
相关题目