题目内容
曲线y=2x﹣x2，y=2x2﹣4x所围成图形的面积为 ．
解答：
[解析]由
由图可知，所求图形的面积为S=
（2x﹣x2）dx+|（2x2﹣4x）dx|=（2x﹣x2）dx﹣（2x2﹣4x）dx．
因为
′=2x﹣x2，
，
所以S=
﹣
．
故答案为：4．
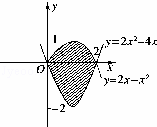
练习册系列答案
相关题目
曲线y=2x-lnx在点（1，2）处的切线方程为（ ）
| A、y=-x-1 | B、y=-x+3 | C、y=x+1 | D、y=x-1 |