题目内容
(2012•唐山二模)直线l与双曲线C:
-
=1(a>0,b>0)交于A、B两点,M是线段AB的中 点,若l与OM (O是原点)的斜率的乘积等于1,则此双曲线的离心率为( )
| ||
|
| ||
|
分析:设A(x1,y1),B(x2,y2),由M是线段AB的中点,知M(
,
),把A(x1,y1),B(x2,y2)分别代入双曲线C:
-
=1(a>0,b>0),得
,故b2(x1+x2)(x1-x2)-a2(y1+y2)(y1-y2)=0,直线l的斜率kl=
,由M(
,
),O(0,0),知OM的斜率kOM=
,由l与OM的斜率的乘积等于1,知a=b,由此能求出此双曲线的离心率.
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
| ||
|
| ||
|
|
| b2(x1 +x2) |
| a2(y1+y2) |
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
| y1+y2 |
| x1+x2 |
解答:解:设A(x1,y1),B(x2,y2),
∵M是线段AB的中点,∴M(
,
),
把A(x1,y1),B(x2,y2)分别代入双曲线C:
-
=1(a>0,b>0),
得
,
∴b2(x1+x2)(x1-x2)-a2(y1+y2)(y1-y2)=0,
∴直线l的斜率kl=
,
∵M(
,
),O(0,0),
∴OM的斜率kOM=
,
∵l与OM的斜率的乘积等于1,
∴
•
=
=1,
∴a=b,
∴此双曲线的离心率e=
.
故选B.
∵M是线段AB的中点,∴M(
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
把A(x1,y1),B(x2,y2)分别代入双曲线C:
| ||
|
| ||
|
得
|
∴b2(x1+x2)(x1-x2)-a2(y1+y2)(y1-y2)=0,
∴直线l的斜率kl=
| b2(x1 +x2) |
| a2(y1+y2) |
∵M(
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
∴OM的斜率kOM=
| y1+y2 |
| x1+x2 |
∵l与OM的斜率的乘积等于1,
∴
| b2(x1+x2) |
| a2(y1+y2) |
| y1+y2 |
| x1+x2 |
| a2 |
| b2 |
∴a=b,
∴此双曲线的离心率e=
| 2 |
故选B.
点评:本题考查双曲线的简单性质的应用,解题时要认真审题,仔细解答,注意点差法的合理运用.

练习册系列答案
相关题目
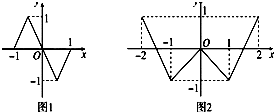 (2012•唐山二模)奇函数f(x)、偶函数g(x)的图象分别如图1、2所示,方程f(g(x))=0、g(f(x))=0的实根个数分别为a、b,则a+b=( )
(2012•唐山二模)奇函数f(x)、偶函数g(x)的图象分别如图1、2所示,方程f(g(x))=0、g(f(x))=0的实根个数分别为a、b,则a+b=( )