题目内容
已知函数f(x)=-|x|+1,若关于x 的方程f2(x)+(2m-l)f(x)+4-2m=0有 4 个不同的实数解,则实数m的取值范围是
- A.m

- B.m
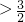
- C.m
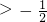
- D.m

B
分析:题中原方程f2(x)+(2m-l)f(x)+4-2m=0有 4 个不同 的实数解,即要求对应于f(x)=某个常数K,有2个不同的K,先根据题意作出f(x)的简图,再根据函数f(x)=-|x|+1对应法则,设t=f(x),等价于方程t2+(2m-l)t+4-2m=0有2个不同 的实数解,再根据一元二次方程根的分布理论可以得出答案.
解答: 解:函数f(x)的图象如右,设t=f(x)∈(-∞,1],
解:函数f(x)的图象如右,设t=f(x)∈(-∞,1],
则关于x 的方程f2(x)+(2m-l)f(x)+4-2m=0有 4 个不同 的实数解,
等价于方程t2+(2m-l)t+4-2m=0有2个不同 的实数解,
设g(t)=t2+(2m-l)t+4-2m,则
 ,
,
解得 ,∴m>
,∴m> .
.
故选B.
点评:本题考查了函数的图象与一元二次方程根的分布的知识,属于难题,采用数形结合的方法解决,使本题变得易于理解.数形结合是数学解题中常用的思想方法,能够变抽象思维为形象思维,有助于把握数学问题的本质;另外,由于使用了数形结合的方法,很多问题便迎刃而解,且解法简捷.
分析:题中原方程f2(x)+(2m-l)f(x)+4-2m=0有 4 个不同 的实数解,即要求对应于f(x)=某个常数K,有2个不同的K,先根据题意作出f(x)的简图,再根据函数f(x)=-|x|+1对应法则,设t=f(x),等价于方程t2+(2m-l)t+4-2m=0有2个不同 的实数解,再根据一元二次方程根的分布理论可以得出答案.
解答:
 解:函数f(x)的图象如右,设t=f(x)∈(-∞,1],
解:函数f(x)的图象如右,设t=f(x)∈(-∞,1],则关于x 的方程f2(x)+(2m-l)f(x)+4-2m=0有 4 个不同 的实数解,
等价于方程t2+(2m-l)t+4-2m=0有2个不同 的实数解,
设g(t)=t2+(2m-l)t+4-2m,则
 ,
,解得
 ,∴m>
,∴m> .
.故选B.
点评:本题考查了函数的图象与一元二次方程根的分布的知识,属于难题,采用数形结合的方法解决,使本题变得易于理解.数形结合是数学解题中常用的思想方法,能够变抽象思维为形象思维,有助于把握数学问题的本质;另外,由于使用了数形结合的方法,很多问题便迎刃而解,且解法简捷.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|