题目内容
已知抛物线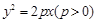 的焦点为
的焦点为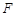 ,点
,点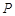 是抛物线上的一点,且其纵坐标为4,
是抛物线上的一点,且其纵坐标为4,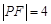 .
.
(1)求抛物线的方程;
(2)设点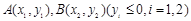 是抛物线上的两点,
是抛物线上的两点,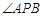 的角平分线与
的角平分线与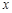 轴垂直,求直线AB的斜率;
轴垂直,求直线AB的斜率;
(3)在(2)的条件下,若直线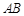 过点
过点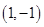 ,求弦
,求弦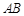 的长.
的长.
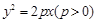 的焦点为
的焦点为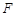 ,点
,点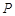 是抛物线上的一点,且其纵坐标为4,
是抛物线上的一点,且其纵坐标为4,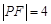 .
.(1)求抛物线的方程;
(2)设点
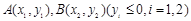 是抛物线上的两点,
是抛物线上的两点,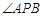 的角平分线与
的角平分线与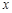 轴垂直,求直线AB的斜率;
轴垂直,求直线AB的斜率;(3)在(2)的条件下,若直线
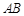 过点
过点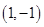 ,求弦
,求弦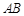 的长.
的长.(1) (2)-1(3)
(2)-1(3)
 (2)-1(3)
(2)-1(3)
试题分析:解:(1)设
 ,因为
,因为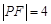 ,由抛物线的定义得
,由抛物线的定义得 ,又
,又 ,所以
,所以 ,因此
,因此 ,解得
,解得 ,从而抛物线的方程为
,从而抛物线的方程为 .
.(2)由(1)知点
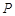 的坐标为
的坐标为 ,因为
,因为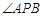 的角平分线与
的角平分线与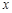 轴垂直,所以可知
轴垂直,所以可知 的倾斜角互补,即
的倾斜角互补,即 的斜率互为相反数
的斜率互为相反数设直线
 的斜率为
的斜率为 ,则
,则 ,由题意
,由题意 ,
,把
 代入抛物线方程得
代入抛物线方程得 ,该方程的解为4、
,该方程的解为4、 ,
,由韦达定理得
 ,即
,即 ,同理
,同理 ,
,所以
 ,
,(3)设
 ,代入抛物线方程得
,代入抛物线方程得 ,
, ,
,点评:关于曲线的大题,第一问一般是求出曲线的方程,第二问常与直线结合起来,当涉及到交点时,常用到根与系数的关系式:
 (
( )。
)。
练习册系列答案
相关题目
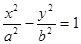 与
与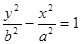 的四个顶点组成的四边形的面积为
的四个顶点组成的四边形的面积为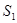 ,连接其四个焦点组成的四边形的面积为
,连接其四个焦点组成的四边形的面积为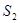 ,则
,则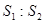 的最大值是
的最大值是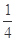
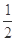
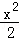 +y2=1有公共的焦点,且它们的离心率互为倒数,则该双曲线的方程是 .
+y2=1有公共的焦点,且它们的离心率互为倒数,则该双曲线的方程是 . 的双曲线的焦点在x轴上,且过点P
的双曲线的焦点在x轴上,且过点P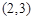 .
. 的焦点为顶点,顶点为焦点的椭圆的标准方程是
的焦点为顶点,顶点为焦点的椭圆的标准方程是 



 =1的两条渐近线互相垂直,那么该双曲线的离心率是 .
=1的两条渐近线互相垂直,那么该双曲线的离心率是 .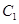 与抛物线
与抛物线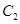 的焦点均在
的焦点均在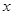 轴上,
轴上,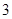
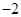
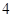
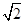
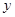
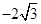

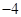
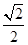
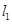 过抛物线
过抛物线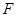 ,
,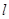 与椭圆交于不同的两点
与椭圆交于不同的两点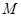 、
、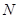 ,当
,当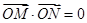 时,求直线
时,求直线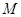 到点
到点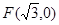 的距离与到直线
的距离与到直线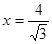 的距离之比为定值
的距离之比为定值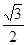 ,记
,记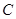 .
.
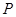 是圆
是圆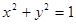 上第一象限内的任意一点,过
上第一象限内的任意一点,过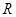 ,
,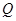 两点.
两点.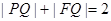 ;
;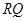 的最大值.
的最大值.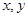 )及两个定点A(-2,0),B(2,0),直线PA、PB的斜率分别为
)及两个定点A(-2,0),B(2,0),直线PA、PB的斜率分别为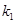 、
、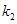 且
且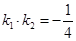
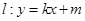 与曲线C交于不同的两点M、N,当OM⊥ON时,求点O到直线
与曲线C交于不同的两点M、N,当OM⊥ON时,求点O到直线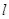 的距离。(O为坐标原点)
的距离。(O为坐标原点)