题目内容
与圆 都相切的直线有( )
都相切的直线有( )
| A.1条 | B.2条 | C.3条 | D.4条 |
A
解析试题分析:两圆方程配方得: ,
, ,∴圆心距
,∴圆心距 =
= ,∴圆
,∴圆 和圆
和圆 相内切,所以与两圆都相切的直线有1条.
相内切,所以与两圆都相切的直线有1条.
考点:平面内两个圆的位置关系.

练习册系列答案
相关题目
已知圆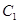 :
: ,圆
,圆 与圆
与圆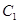 关于直线
关于直线 对称,则圆
对称,则圆 的方程为 ( )
的方程为 ( )
A. | B. |
C. | D. |
设椭圆 的离心率为
的离心率为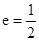 ,右焦点为
,右焦点为 ,方程
,方程 的两个实根分别为
的两个实根分别为 和
和 ,则点
,则点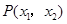 ( )
( )
A.必在圆 内 内 | B.必在圆 上 上 |
C.必在圆 外 外 | D.以上三种情形都有可能 |
过点 作圆
作圆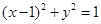 的两条切线,切点分别为
的两条切线,切点分别为 ,
, ,则直线
,则直线 的方程为( )
的方程为( )
A. | B. | C. | D.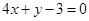 |
垂直于直线 与圆
与圆 相切于第一象限的直线方程是( )
相切于第一象限的直线方程是( )
A. | B. | C. | D. |
直线 与圆
与圆 相切,则实数
相切,则实数 等于( )
等于( )
A. 或 或 | B. 或 或 | C. 或 或 | D. 或 或 |
在平面直角坐标系 中,直线
中,直线 与圆
与圆 相交于
相交于 两点,则弦
两点,则弦 的长等于( )
的长等于( )
A. | B. | C. | D. |
若直线 始终平分圆
始终平分圆 的周长,则
的周长,则 的最小值为( )
的最小值为( )
A. | B. | C. | D.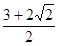 |
圆 :
: 与圆
与圆 :
: 的位置关系( )
的位置关系( )
| A.相交 | B.外切 | C.内切 | D.外离 |