题目内容

（2012•泉州模拟）四棱锥P-ABCD的顶点P在底面ABCD上的投影恰好是A，其正视图与侧视图都是腰长为a的等腰直角三角形．则在四棱锥P-ABCD的任意两个顶点的连线中，互相垂直的异面直线共有
6
6
对．
分析：由题设知四棱锥P-ABCD中，PA⊥面ABCD，ABCD是边长为a的正方形，PA=a，由此能求出在四棱锥P-ABCD的任意两个顶点的连线中，互相垂直的异面直线有多少对．
解答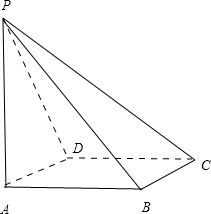：解：∵四棱锥P-ABCD的顶点P在底面ABCD上的投影恰好是A，
其正视图与侧视图都是腰长为a的等腰直角三角形，
∴四棱锥P-ABCD中，PA⊥面ABCD，ABCD是边长为a的正方形，PA=a，（如图）
∴在四棱锥P-ABCD的任意两个顶点的连线中，互相垂直的异面直线有：
PA和CD，PA和BC，PD和BC，PD和AB，PB和AD，PB和AD，共6对．
故答案为：6．
点评：本题考查异面直线的判定，具体涉及到空间几何体的三视图，四棱锥的结构特征等基本知识点，是基础题．解题时要认真审题，仔细解答．
练习册系列答案
相关题目
（2012•泉州模拟）已知f0(x)=x•ex，f1（x）=f′0（x），f2（x）=f′1（x），…，fn（x）=f′n-1（x）（n∈N*）．
（Ⅰ）请写出fn（x）的表达式（不需证明）；
（Ⅱ）设fn（x）的极小值点为Pn（xn，yn），求yn；
（Ⅲ）设gn(x)=-x2-2(n+1)x-8n+8，gn（x）的最大值为a，fn（x）的最小值为b，试求a-b的最小值．
（2012•泉州模拟）下列函数中，既是偶函数，且在区间（0，+∞）内是单调递增的函数是（　　）
（2012•泉州模拟）已知集合A={1，2，3}，B={x|x2-x-2=0，x∈R}，则A∩B为（　　）
（2012•泉州模拟）设函数f（x）=ax2+lnx．
（Ⅰ）当a=-1时，求函数y=f（x）的图象在点（1，f（1））处的切线方程；
（Ⅱ）已知a＜0，若函数y=f（x）的图象总在直线y=-
12
的下方，求a的取值范围；
（Ⅲ）记f′（x）为函数f（x）的导函数．若a=1，试问：在区间[1，10]上是否存在k（k＜100）个正数x1，x2，x3…xk，使得f′（x1）+f'（x2）+f′（x3）+…+f′（xk）≥2012成立？请证明你的结论．
（2012•泉州模拟）设函数y=f（x）的定义域为D，若对于任意x1，x2∈D且x1+x2=2a，恒有f（x1）+f（x2）=2b，则称点（a，b）为函数y=f（x）图象的对称中心．研究并利用函数f（x）=x3-3x2-sin（πx）的对称中心，可得f(
1
2012
)+f(
2
2012
)+…+f(
4022
2012
)+f(
4023
2012
)=（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网