Question

国家对空气质量的分级规定如下表：

污染指数	0～50	51～100	101～150	151～200	201～300	＞300
空气质量	优	良	轻度污染	中度污染	重度污染	严重污染

某市去年6月份30天的空气污染指数的监测数据如下：

34	140	18	73	121	210	40	45	78	23	65	79	207	81	60
42	101	38	163	154	22	27	36	151	49	103	135	20	16	48

根据以上信息，解决下列问题：
（Ⅰ）写出下面频率分布表中a，b，x，y的值；
（Ⅱ）某人计划今年6月份到此城市观光4天，若将（Ⅰ）中的频率作为概率，他遇到空气质量为优或良的天数用X表示，求X的分布列和均值EX．

频率分布表
分组	频数	频率
[0，50]	14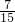
（50，100]	a	x
（100，150]	5
（150，200]	b	y
（200，250]	2
合计	30	1

Answer 1

解：（I）由某市去年6月份30天的空气污染指数的监测数据表知，
，…．（4分）
（Ⅱ）由题意，该市4月份空气质量为优或良的概率为P=，…..（5分）
，，，，．…．（10分）
∴X的分布列为：

X	0	1	2	3	4
P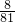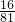

…．（11分）
∵X～B（4，），
∴．…．（13分）
分析：（I）某市去年6月份30天的空气污染指数的监测数据，即可得到频率分布表中a，b，x，y的值；
（II）确定X的可能取值，再利用组合数确定相应的频率，即可求X的分布列和数学期望EX．
点评：本题考查离散型随机变量的期望与方差，考查读频数分布直方图的能力和利用统计图获取信息的能力．利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题．