题目内容
点M（a，b）在函数
的图象上，点N与点M关于y轴对称且在直线x-y+3=0上，则函数f（x）=abx2+（a+b）x-1在区间[-2，2）上
- A.既没有最大值也没有最小值
- B.最小值为-3，无最大值
- C.最小值为-3，最大值为9
- D.最小值为
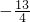，无最大值
D
分析：本题应先根据对称性建立关于a，b的方程，解出a，b的值，代入函数的表达式，利用函数的表达式研究函数在区间[-2，2）上的单调性，用单调性判断出函数在区间上的最大值与最小值．
解答：点M（a，b）在函数的图象上，故有b=
①
点N与点M关于y轴对称，故点N（-a，b），又点N在直线x-y+3=0上，故-a-b+3=0 ②
由①②得ab=1，a+b=3
函数f（x）=x2+3x-1
其对称轴为x=-
∈[-2，2）
故函数f（x）在[-2，2）上的最大值为不存在，最小值为f（-）=-
故应选 D．
点评：考查函数的最值，二次函数的最值问题是考试的热点，本题在考查二次函数求最值与图象的对称性结合来考，有形有数形式新颖．
分析：本题应先根据对称性建立关于a，b的方程，解出a，b的值，代入函数的表达式，利用函数的表达式研究函数在区间[-2，2）上的单调性，用单调性判断出函数在区间上的最大值与最小值．
解答：点M（a，b）在函数
的图象上，故有b=①点N与点M关于y轴对称，故点N（-a，b），又点N在直线x-y+3=0上，故-a-b+3=0 ②
由①②得ab=1，a+b=3
函数f（x）=x2+3x-1
其对称轴为x=-
∈[-2，2）故函数f（x）在[-2，2）上的最大值为不存在，最小值为f（-
）=-故应选 D．
点评：考查函数的最值，二次函数的最值问题是考试的热点，本题在考查二次函数求最值与图象的对称性结合来考，有形有数形式新颖．
练习册系列答案
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
相关题目
若点M（a，b）在函数y=
（-1≤x≤0）的图象上，则下列哪个函数的图象一定经过点N（b，a）（ ）
| 1-x2 |
A、y=
| ||
B、y=-
| ||
C、y=-
| ||
D、y=
|
点M（a，b）在函数y=
的图象上，点N与点M关于y轴对称且在直线x-y+3=0上，则函数f（x）=abx2+（a+b）x-1在区间[-2，2）上（ ）
| 1 |
| x |
| A、既没有最大值也没有最小值 | ||
| B、最小值为-3，无最大值 | ||
| C、最小值为-3，最大值为9 | ||
D、最小值为-
|
（-1≤x≤0）的图象上，则下列哪个函数的图象一定经过点N（b，a）（ ）
（-1≤x≤0）
（0≤x≤1）
（-1≤x≤0）
（0≤x≤1）
的图象上，点N与点M关于y轴对称且在直线x-y+3=0上，则函数f（x）=abx2+（a+b）x-1在区间[-2，2）上（ ）
，无最大值
的图象上，点N与点M关于y轴对称且在直线x-y+3=0上，则函数f（x）=abx2+（a+b）x-1在区间[-2，2）上（ ）
，无最大值