题目内容
已知函数f(x)=2lnx-x2+ax,a∈R.
(1)当a=2时,求函数f(x)的图象在x=1处的切线的方程;
(2)若函数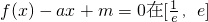 上有两个不等的实数根,求实数m的取值范围;
上有两个不等的实数根,求实数m的取值范围;
(3)若函数f(x)的图象与x轴交于不同的点A(x1,0),B(x2,0),且0<x1<x2,求证:f′(px1+qx2)<0(其中实数p,q满足0<p≤q,p+q=1)
解:(1)当a=2时,f(x)=2lnx-x2+2x,
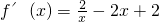 ,切点坐标为(1,1),切线的斜率k=f'(1)=2,
,切点坐标为(1,1),切线的斜率k=f'(1)=2,
则切线方程为y-1=2(x-1),即y=2x-1.(2分)
(2)方程f(x)-ax+m=0即为2lnx-x2+m=0,
令g(x)=2lnx-x2+m,则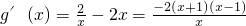 ,
,
因为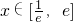 ,故g'(x)=0时,x=1.
,故g'(x)=0时,x=1.
当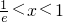 时,g'(x)>0;当1<x<e时,g'(x)<0.
时,g'(x)>0;当1<x<e时,g'(x)<0.
故函数g(x)在x=1处取得极大值g(1)=m-1,(4分)
又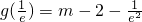 ,g(e)=m+2-e2,
,g(e)=m+2-e2,
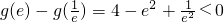 ,则
,则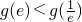 ,
,
故函数g(x)在 上的最小值是g(e).(6分)
上的最小值是g(e).(6分)
方程f(x)-ax+m=0在 上有两个不相等的实数根,则有
上有两个不相等的实数根,则有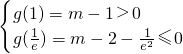
解得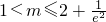 ,故实数m的取值范围是
,故实数m的取值范围是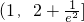 .(8分)
.(8分)
(3)∵函数f(x)的图象与x轴交于两个不同的点A(x1,0),B(x2,0),2lnx-x2+ax=0的两个根为x1,x2,
则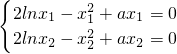 两式相减得
两式相减得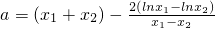 ,f(x)=2lnx-x2+ax,
,f(x)=2lnx-x2+ax,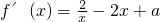 ,
,
则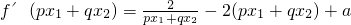 =
=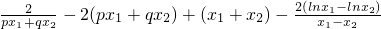
=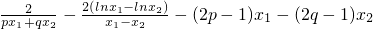
=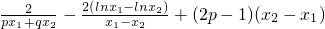 .(*)(10分)
.(*)(10分)
∵0<p≤q,p+q=1,则2p≤1,又0<x1<x2,∴(2p-1)(x2-x1)≤0,
下证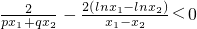 ,即证明
,即证明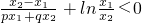 .
.
令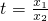 ,∵0<x1<x2,∴0<t<1,
,∵0<x1<x2,∴0<t<1,
即证明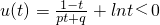 在0<t<1上恒成立,(12分)
在0<t<1上恒成立,(12分)
∵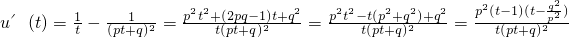 ,
,
∵0<p≤q,∴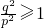 ,又0<t<1,∴u'(t)>0,
,又0<t<1,∴u'(t)>0,
∴u(t)在(0,1)上是增函数,则u(t)<u(1)=0,从而知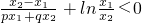 ,
,
故(*)<0,即f'(px1+qx2)<0成立.(14分)
分析:(1)先求出切点坐标,然后利用导数求出k=f'(1),最后根据点斜式求出切线方程即可;
(2)方程f(x)-ax+m=0即为2lnx-x2+m=0,令g(x)=2lnx-x2+m,利用导数研究该函数在 上的最小值,要使方程f(x)-ax+m=0在
上的最小值,要使方程f(x)-ax+m=0在 上有两个不相等的实数根,则有
上有两个不相等的实数根,则有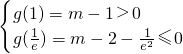 ,解之即可;
,解之即可;
(3)将a用x1与x2表示,然后求出导函数f′(x),从而得到f′(px1+qx2),然后利用导数研究函数的单调性证明f′(px1+qx2)<0.
点评:本题主要考查了利用导数研究曲线上某点切线方程,以及利用导数研究函数的单调性,同时考查了转化的思想和计算能力,属于难题.
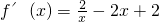 ,切点坐标为(1,1),切线的斜率k=f'(1)=2,
,切点坐标为(1,1),切线的斜率k=f'(1)=2,则切线方程为y-1=2(x-1),即y=2x-1.(2分)
(2)方程f(x)-ax+m=0即为2lnx-x2+m=0,
令g(x)=2lnx-x2+m,则
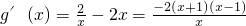 ,
,因为
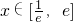 ,故g'(x)=0时,x=1.
,故g'(x)=0时,x=1.当
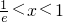 时,g'(x)>0;当1<x<e时,g'(x)<0.
时,g'(x)>0;当1<x<e时,g'(x)<0.故函数g(x)在x=1处取得极大值g(1)=m-1,(4分)
又
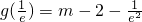 ,g(e)=m+2-e2,
,g(e)=m+2-e2,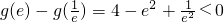 ,则
,则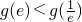 ,
,故函数g(x)在
 上的最小值是g(e).(6分)
上的最小值是g(e).(6分)方程f(x)-ax+m=0在
 上有两个不相等的实数根,则有
上有两个不相等的实数根,则有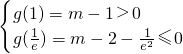
解得
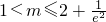 ,故实数m的取值范围是
,故实数m的取值范围是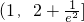 .(8分)
.(8分)(3)∵函数f(x)的图象与x轴交于两个不同的点A(x1,0),B(x2,0),2lnx-x2+ax=0的两个根为x1,x2,
则
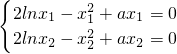 两式相减得
两式相减得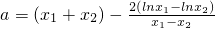 ,f(x)=2lnx-x2+ax,
,f(x)=2lnx-x2+ax,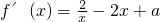 ,
,则
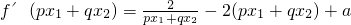 =
=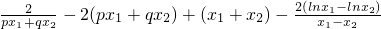
=
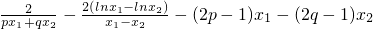
=
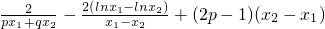 .(*)(10分)
.(*)(10分)∵0<p≤q,p+q=1,则2p≤1,又0<x1<x2,∴(2p-1)(x2-x1)≤0,
下证
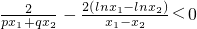 ,即证明
,即证明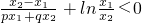 .
.令
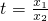 ,∵0<x1<x2,∴0<t<1,
,∵0<x1<x2,∴0<t<1,即证明
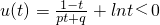 在0<t<1上恒成立,(12分)
在0<t<1上恒成立,(12分)∵
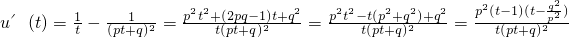 ,
,∵0<p≤q,∴
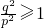 ,又0<t<1,∴u'(t)>0,
,又0<t<1,∴u'(t)>0,∴u(t)在(0,1)上是增函数,则u(t)<u(1)=0,从而知
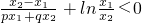 ,
,故(*)<0,即f'(px1+qx2)<0成立.(14分)
分析:(1)先求出切点坐标,然后利用导数求出k=f'(1),最后根据点斜式求出切线方程即可;
(2)方程f(x)-ax+m=0即为2lnx-x2+m=0,令g(x)=2lnx-x2+m,利用导数研究该函数在
 上的最小值,要使方程f(x)-ax+m=0在
上的最小值,要使方程f(x)-ax+m=0在 上有两个不相等的实数根,则有
上有两个不相等的实数根,则有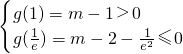 ,解之即可;
,解之即可;(3)将a用x1与x2表示,然后求出导函数f′(x),从而得到f′(px1+qx2),然后利用导数研究函数的单调性证明f′(px1+qx2)<0.
点评:本题主要考查了利用导数研究曲线上某点切线方程,以及利用导数研究函数的单调性,同时考查了转化的思想和计算能力,属于难题.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目