题目内容
5.在三角形ABC中,角A,B,C所对的边分别是a、b、c,且sin2B=sin2A+sin2C-sinAsinC.(1)求角B的值;
(2)若b=$\sqrt{3}$,S△ABC=$\frac{\sqrt{3}}{2}$,求$\overrightarrow{BA}$•$\overrightarrow{BC}$及a+c的值.
分析 (1)由正弦定理可得b2=a2+c2-ac,整体代入余弦定理可得cosB,可得B;
(2)由题意和三角形的面积公式可得ac,进而可得数量积,再由余弦定理整体可解a+c.
解答 解:(1)在△ABC中,∵在三角形ABC中sin2B=sin2A+sin2C-sinAsinC,
∴由正弦定理可得b2=a2+c2-ac,∴a2+c2-b2=ac,
∴由余弦定理可得cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{ac}{2ac}$=$\frac{1}{2}$,
由0<B<π可得B=$\frac{π}{3}$;
(2)∵S△ABC=$\frac{1}{2}$acsinB=$\frac{1}{2}$ac•$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$,∴ac=2,
∴$\overrightarrow{BA}$•$\overrightarrow{BC}$=accosB=2×$\frac{1}{2}$=1,
再由余弦定理可得b2=a2+c2-2accosB=(a+c)2-3ac,
∴(a+c)2=b2+3ac=9,∴a+c=3
点评 本题考查正余弦定理解三角形,涉及三角形的面积公式和向量的运算,属中档题.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
15.如图,在四面体ABCD中,设G是CD的中点,则$\overrightarrow{AB}+\frac{1}{2}(\overrightarrow{BD}+\overrightarrow{BC})$等于( )
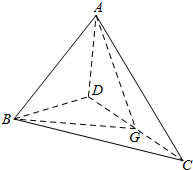

| A. | $\overrightarrow{AD}$ | B. | $\overrightarrow{BG}$ | C. | $\overrightarrow{CD}$ | D. | $\overrightarrow{AG}$ |
10.某校羽毛球小组有男学生A,B,C和女学生X,Y,Z共6人,其所属年级如下:
现从这6名学生中随机选出2人参加羽毛球比赛(每人被选到的可能性相同).
(1)共有几种不同的选法?用表中字母列举出来;
(2)设M为事件“选出的2人性别相同”,求事件M发生的概率.
| 一年级 | 二年级 | 三年级 | |
| 男生 | A | B | C |
| 女生 | X | Y | Z |
(1)共有几种不同的选法?用表中字母列举出来;
(2)设M为事件“选出的2人性别相同”,求事件M发生的概率.