题目内容
若θ是三角形的一个内角,且m=sinθ+cosθ,则“0<m<1”是“方程x2sinθ+y2cosθ=1表示的曲线是双曲线”的( )
分析:利用m=sinθ+cosθ,两边平方m2=1+2sinθcosθ,结合θ是三角形的一个内角,可知充分性成立;当θ=
时,方程x2sinθ+y2cosθ=1表示的曲线是双曲线,但是m=sinθ+cosθ=0,故可得结论.
| 3π |
| 4 |
解答:解:∵m=sinθ+cosθ,∴m2=1+2sinθcosθ
∵0<m<1,∴sinθcosθ<0
∵θ是三角形的一个内角,∴sinθ>0,cosθ<0
∴方程x2sinθ+y2cosθ=1表示的曲线是双曲线
∴“0<m<1”是“方程x2sinθ+y2cosθ=1表示的曲线是双曲线”的充分条件
当θ=
时,方程x2sinθ+y2cosθ=1表示的曲线是双曲线,但是m=sinθ+cosθ=0
∴“0<m<1”不是“方程x2sinθ+y2cosθ=1表示的曲线是双曲线”的必要条件
∴“0<m<1”是“方程x2sinθ+y2cosθ=1表示的曲线是双曲线”的充分不必要条件
故选A.
∵0<m<1,∴sinθcosθ<0
∵θ是三角形的一个内角,∴sinθ>0,cosθ<0
∴方程x2sinθ+y2cosθ=1表示的曲线是双曲线
∴“0<m<1”是“方程x2sinθ+y2cosθ=1表示的曲线是双曲线”的充分条件
当θ=
| 3π |
| 4 |
∴“0<m<1”不是“方程x2sinθ+y2cosθ=1表示的曲线是双曲线”的必要条件
∴“0<m<1”是“方程x2sinθ+y2cosθ=1表示的曲线是双曲线”的充分不必要条件
故选A.
点评:本题考查四种条件的判定,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
 =2”.若把该结论推广到正四面体(所有棱长均相等的三棱锥),则有结论:“在正四面体ABCD中,若M是正三角形BCD的中心,O是在正四面体ABCD内切球的球心,则
=2”.若把该结论推广到正四面体(所有棱长均相等的三棱锥),则有结论:“在正四面体ABCD中,若M是正三角形BCD的中心,O是在正四面体ABCD内切球的球心,则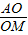 = ”.
= ”. ,那么这个球的表面积是 .
,那么这个球的表面积是 .