题目内容
设c,d,x为实数,c≠0,x为未知数,讨论方程log(cx+
)x=-1在什么情况下有解,有解时求出它的解.
| d |
| x |
原方程有解的充要条件是:
由条件(4)知x(cx+
)=1,所以cx2+d=1再由c≠0,可得x2=
.
又由x(cx+
)=1及x>0,知cx+
>0,
即条件(2)包含在条件(1)及(4)中
再由条件(3)及x(cx+
)=1,知x≠1
因此,原条件可简化为以下的等价条件组:
由条件(1)(6)知
>0.这个不等式仅在以下两种情形下成立:
①c>0,1-d>0,即c>0,d<1;
②c<0,1-d<0,即c<0,d>1、
再由条件(1)(5)及(6)可知c≠1-d
从而,当c>0,d<1且c≠1-d时,
或者当c<0,d>1且c≠1-d时,
原方程有解,它的解是x=
|
由条件(4)知x(cx+
| d |
| x |
| 1-d |
| c |
又由x(cx+
| d |
| x |
| d |
| x |
即条件(2)包含在条件(1)及(4)中
再由条件(3)及x(cx+
| d |
| x |
因此,原条件可简化为以下的等价条件组:
|
由条件(1)(6)知
| 1-d |
| c |
①c>0,1-d>0,即c>0,d<1;
②c<0,1-d<0,即c<0,d>1、
再由条件(1)(5)及(6)可知c≠1-d
从而,当c>0,d<1且c≠1-d时,
或者当c<0,d>1且c≠1-d时,
原方程有解,它的解是x=
|

练习册系列答案
相关题目



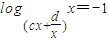 在什么情况下有解,有解时求出它的解.
在什么情况下有解,有解时求出它的解.