题目内容

设a＞2,给定数列{xn},其中x1=a,xn+1=(n∈N*).求证:

(1)xn＞2,且xn+1＜xn(n∈N*);

(2)如果2＜a≤3,那么xn≤2+(n∈N*).

证明:(1)使用数学归纳法证明xn＞2.

当n=1时,x1=a＞2命题成立;假设当n=k(k∈N*)时命题成立,即xn＞2.

当n=k+1时,xn+1-2==＞0,即xn+1＞2.

综上,对一切n∈N*,有xn＞2.

当xn＞2时,==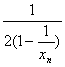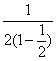＜=1.所以xn+1＜xn(n∈N*).

(2)因为xn＞2,所以=1∈(0,1).

故xn+1-2==(xn-2)()＜(xn-2)(n∈N*).

由此可得xn-2≤(xn-1-2)≤(xn-2-2)≤…≤(x1-2)=(a-2),

xn≤2+.

所以当2＜a≤3时,xn≤2+(n∈N*).

练习册系列答案
相关题目
设a＞2，给定数列{xn}，其中x1=a，xn+1=
x
2
n
2(xn-1)
(n=1，2…)求证：
（1）xn＞2，且
xn+1
xn
＜1(n=1，2…)；
（2）如果a≤3，那么xn≤2+
1
2n-1
(n=1，2…)．
设a＞2，给定数列{an}，a1=a，an+1=
an22(an-1)
（n∈N+）．求证：an＞2，且an+1＜an（n∈N+）．
设a＞2，给定数列{an}，a1=a，an+1an=an+1+
1
2
a
2
n
(n∈N*)
（1）求证：an＞2；
（2）求证：数列{an}是单调递减数列．
设a＞2，给定数列{xn}，其中x 1=a，xn+1=
x
2
n
2(xn-1)
(n∈N*)求证：
（1）xn＞2，且xn+1＜xn（n∈N*）；
（2）如果2＜a≤3，那么xn≤2+
1
2n-1
(n∈N*)．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网