题目内容
已知数列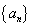 中,
中,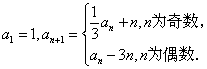
(I)求证:数列 是等比数列;
是等比数列;
(II)若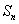 是数列
是数列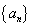 的前n项和,求满足
的前n项和,求满足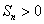 的所有正整数n.
的所有正整数n.
解:(Ⅰ)设 ,
,
因为
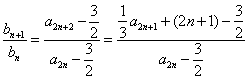 =
=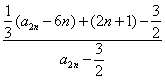 =
=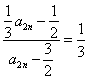 ,
,
所以数列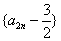 是以
是以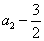 即
即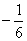 为首项,以
为首项,以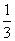 为公比的等比数列. ……… 5分
为公比的等比数列. ……… 5分
(Ⅱ)由(Ⅰ)得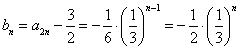 ,即
,即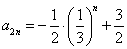 ,
,
由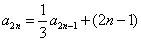 ,得
,得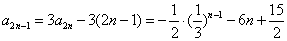 ,
,
所以
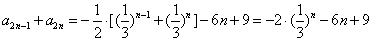 ,
,
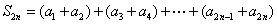
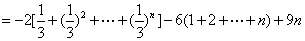


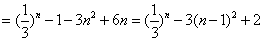 10分
10分
显然当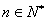 时,
时,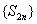 单调递减,
单调递减,
又当 时,
时,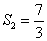 >0,当
>0,当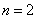 时,
时,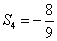 <0,所以当
<0,所以当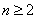 时,
时,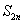 <0;
<0;
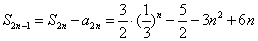 ,
,
同理,当且仅当 时,
时,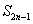 >0,
>0,
综上,满足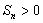 的所有正整数
的所有正整数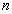 为1和2.…………………………………… 12分
为1和2.…………………………………… 12分

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
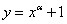 (α∈R)在点(1,2)处的切线经过坐标原点,则α=_________.
(α∈R)在点(1,2)处的切线经过坐标原点,则α=_________.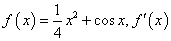 是函数
是函数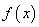 的导函数,则
的导函数,则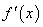 的图象大致是
的图象大致是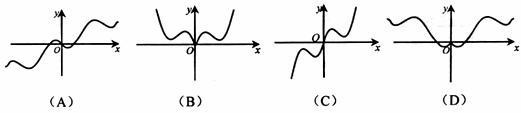
 是边BC上的高,则
是边BC上的高,则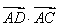 的值等于
的值等于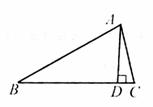
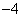
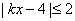 的解集为
的解集为 ,则实数
,则实数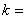 .
.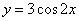 的图象,只需把函数
的图象,只需把函数 的图象上所有的点
的图象上所有的点 个单位 B.向右平移
个单位 B.向右平移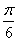 个单位
个单位 ,那么
,那么 等于 ( )
等于 ( ) B.
B.  C.
C. D.
D.