题目内容
等比数列{an}的各项都为正,公比q=2,且a1a2a3…a30=230,则a3a6a9…a30等于( )
| A、210 | B、215 | C、220 | D、230 |
分析:由等比数列的性质,可将此数列的前三十项分为三组,每组十个数的乘积,第一组是a1a4a7…a28,第二组是a2a5a8…a29,第三组是a3a6a9…a30.此三个数是一个公比为210,由此关系求出答案.
解答:解:由题意可将此数列的前三十项分为三组,每组十个数的乘积,
第一组是a1a4a7…a28,第二组是a2a5a8…a29,第三组是a3a6a9…a30.此三个数是一个公比为210,
令t=a3a6a9…a30,则有a1a4a7…a28=
,a2a5a8…a29=
.
故有t×
×
=230,解得t=220,
即a3a6a9…a30=220,
故选C
第一组是a1a4a7…a28,第二组是a2a5a8…a29,第三组是a3a6a9…a30.此三个数是一个公比为210,
令t=a3a6a9…a30,则有a1a4a7…a28=
| t |
| 220 |
| t |
| 210 |
故有t×
| t |
| 210 |
| t |
| 220 |
即a3a6a9…a30=220,
故选C
点评:本题考查等比数列的性质,解题的关键是熟练掌握数列的性质,且能根据这些性质将本题中涉及的项的乘积表示出来.代入已知的方程求值.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
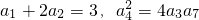 ,则数列{an}的通项公式为________.
,则数列{an}的通项公式为________. ,则数列{an}的通项公式为 .
,则数列{an}的通项公式为 .