题目内容
 如图所示,正方形OACB内的阴影区域的上边界是曲线y=sinx,现向正方形区域内随机等可能地投点,则点落在阴影区域的概率是( )
如图所示,正方形OACB内的阴影区域的上边界是曲线y=sinx,现向正方形区域内随机等可能地投点,则点落在阴影区域的概率是( )分析:根据积分求解出阴影部分的面积,然后再求解正方形的面积,再将它们代入几何概型计算公式计算出概率.
解答:解:阴影部分面积S阴影=∫0π(sinx)dx=(-cosx)|0π=-cosπ+cos0=2
正方形部分面积S=π2
∴所投的点落在阴影部分的概率P=
=
故选D
正方形部分面积S=π2
∴所投的点落在阴影部分的概率P=
| S阴影 |
| S正方形 |
| 2 |
| π2 |
故选D
点评:本题考查几何概型的概率,可以为长度、面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案
相关题目
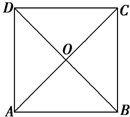 如图所示,在边长为4的正方形纸片ABCD中,AC与BD相交于O,剪去△AOB,将剩余部分沿OC、OD折叠,使OA、OB重合,则以A、(B)、C、D、O为顶点的四面体的体积为
如图所示,在边长为4的正方形纸片ABCD中,AC与BD相交于O,剪去△AOB,将剩余部分沿OC、OD折叠,使OA、OB重合,则以A、(B)、C、D、O为顶点的四面体的体积为
 如图所示,在边长为4的正方形纸片ABCD中,AC与BD相交于O,剪去
如图所示,在边长为4的正方形纸片ABCD中,AC与BD相交于O,剪去 如图所示,在边长为4的正方形纸片ABCD中,AC与BD相交于O,剪去
如图所示,在边长为4的正方形纸片ABCD中,AC与BD相交于O,剪去 如图所示,在边长为4的正方形纸片ABCD中,AC与BD相交于O,剪去
如图所示,在边长为4的正方形纸片ABCD中,AC与BD相交于O,剪去 ,将剩余部分沿OC、OD折叠,使OA、OB重合,则以A、(B)、C、D、O为顶点的四面体的体积为
,将剩余部分沿OC、OD折叠,使OA、OB重合,则以A、(B)、C、D、O为顶点的四面体的体积为