题目内容
设数列{an}的前n项和为Sn,且a1=1,Sn=nan- n(n-1),n∈N*.
n(n-1),n∈N*.
(1)求数列{an}的通项公式;
(2)是否存在自然数n,使S1+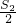 +
+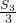 +…+
+…+ =63?若存在,求出n的值;若不存在,说明理由.
=63?若存在,求出n的值;若不存在,说明理由.
解:(1)∵Sn=nan- n(n-1),
n(n-1),
∴n≥2时,Sn-1=(n-1)an-1- (n-1)(n-2),
(n-1)(n-2),
∴两式相减可得:an-an-1=3,
∴数列{an}是首项为1,公差为3的等差数列,
∴an=1+(n-1)•3=3n-2;
(2)Sn=nan- n(n-1)=
n(n-1)=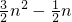 ,∴
,∴ =
=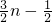
∴数列{ }是以1为首项,
}是以1为首项, 为公差的等差数列
为公差的等差数列
∴S1+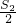 +
+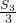 +…+
+…+ =n+
=n+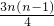 =
=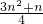
令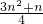 =63,则n=9.
=63,则n=9.
分析:(1)再写一式,两式相减,可得an-an-1=3,即数列{an}是首项为1,公差为3的等差数列,由此能求出数列{an}的通项公式;
(2)确定数列{ }是以1为首项,
}是以1为首项, 为公差的等差数列,利用等差数列的求和公式,即可求得结论.
为公差的等差数列,利用等差数列的求和公式,即可求得结论.
点评:本题考查数列递推式,考查等差数列的判定,考查学生的计算能力,属于中档题.
 n(n-1),
n(n-1),∴n≥2时,Sn-1=(n-1)an-1-
 (n-1)(n-2),
(n-1)(n-2),∴两式相减可得:an-an-1=3,
∴数列{an}是首项为1,公差为3的等差数列,
∴an=1+(n-1)•3=3n-2;
(2)Sn=nan-
 n(n-1)=
n(n-1)=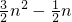 ,∴
,∴ =
=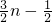
∴数列{
 }是以1为首项,
}是以1为首项, 为公差的等差数列
为公差的等差数列∴S1+
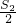 +
+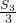 +…+
+…+ =n+
=n+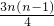 =
=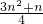
令
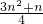 =63,则n=9.
=63,则n=9.分析:(1)再写一式,两式相减,可得an-an-1=3,即数列{an}是首项为1,公差为3的等差数列,由此能求出数列{an}的通项公式;
(2)确定数列{
 }是以1为首项,
}是以1为首项, 为公差的等差数列,利用等差数列的求和公式,即可求得结论.
为公差的等差数列,利用等差数列的求和公式,即可求得结论.点评:本题考查数列递推式,考查等差数列的判定,考查学生的计算能力,属于中档题.

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目