题目内容
 如图,线段AB=8,点C在线段AB上,且AC=2,P为线段CB上一动点,点A绕着C旋转后与点B绕点P旋转后重合于点D,设CP=x,△CPD的面积为f(x).
如图,线段AB=8,点C在线段AB上,且AC=2,P为线段CB上一动点,点A绕着C旋转后与点B绕点P旋转后重合于点D,设CP=x,△CPD的面积为f(x).(1)求x的取值范围;
(2)求f(x)的最大值.
分析:(1)利用三角形的构成条件,建立不等式,可求x的取值范围;
(2)三角形的周长是一个定值8,故其面积可用海伦公式表示出来,再利用基本不等式,即可求f(x)的最大值.
(2)三角形的周长是一个定值8,故其面积可用海伦公式表示出来,再利用基本不等式,即可求f(x)的最大值.
解答:解:(1)由题意,DC=2,CP=x,DP=6-x,根据三角形的构成条件可得
,解得2<x<4;
(2)三角形的周长是一个定值8,故其面积可用海伦公式表示出来,即f(x)=
=2
×
≤2
×
=2
,
当且仅当4-x=-2+x,即x=3时,f(x)的最大值为2
.
|
(2)三角形的周长是一个定值8,故其面积可用海伦公式表示出来,即f(x)=
| 4×(4-x)×(4-6+x)×2 |
=2
| 2 |
| (4-x)(-2+x) |
| 2 |
| 4-x-2+x |
| 2 |
| 2 |
当且仅当4-x=-2+x,即x=3时,f(x)的最大值为2
| 2 |
点评:本题考查根据实际问题选择函数类型,本题中求函数解析式用到了海伦公式,

练习册系列答案
相关题目
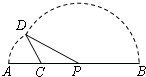 如图,线段AB=8,点C在线段AB上,且AC=2,P为线段CB上一动点,点A绕点C旋转后与点B绕点P旋转后重合于点D.设CP=x,△CPD的面积为f(x).则f(x)的定义域为
如图,线段AB=8,点C在线段AB上,且AC=2,P为线段CB上一动点,点A绕点C旋转后与点B绕点P旋转后重合于点D.设CP=x,△CPD的面积为f(x).则f(x)的定义域为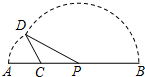 如图,线段AB=8,点C在线段AB上,且AC=2,P为线段CB上一动点,点A绕点C旋转后与点B绕点P旋转后重合于点D.设CP=x,△CPD的面积为f(x).则f(x)的定义域为
如图,线段AB=8,点C在线段AB上,且AC=2,P为线段CB上一动点,点A绕点C旋转后与点B绕点P旋转后重合于点D.设CP=x,△CPD的面积为f(x).则f(x)的定义域为 如图,线段AB=8,点C在线段AB上,且AC=2,P为线段BC上的一动 点,点A绕点C旋转后与点B绕点P旋转后重合于点D,设CP=x,△PCD的面积为f(x),则f(x)的最大值为
如图,线段AB=8,点C在线段AB上,且AC=2,P为线段BC上的一动 点,点A绕点C旋转后与点B绕点P旋转后重合于点D,设CP=x,△PCD的面积为f(x),则f(x)的最大值为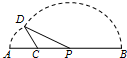 如图,线段AB=8,点C在线段AB上,且AC=2,P为线段CB上一动点,点A绕点C旋转后与点B绕点P旋转后重合于点D.设CP=x,△CPD的面积为f(x).则f(x)的最大值为( )
如图,线段AB=8,点C在线段AB上,且AC=2,P为线段CB上一动点,点A绕点C旋转后与点B绕点P旋转后重合于点D.设CP=x,△CPD的面积为f(x).则f(x)的最大值为( )