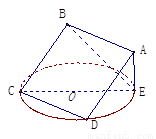
题目内容
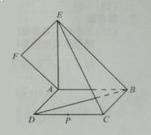
如图,正方形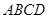 所在平面与圆
所在平面与圆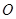 所在平面相交于
所在平面相交于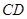 ,线段
,线段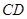 为圆
为圆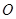 的弦,
的弦,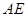 垂直于圆
垂直于圆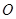 所在平面,垂足
所在平面,垂足 是圆
是圆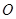 上异于
上异于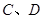 的点,
的点,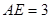 ,圆
,圆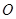 的直径为
的直径为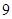 ,
,
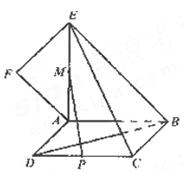
1)求证:平面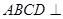 平面
平面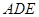 2)求二面角
2)求二面角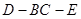 的平面角的正切值.(12分)
的平面角的正切值.(12分)
【答案】
(1)略
(2)
【解析】解:
1)因为 垂直于圆
垂直于圆 所在平面,
所在平面, 在圆
在圆 所在平面上
所在平面上
所以
在正方形
因为 ,所以
,所以
因为
所以
2)因为 ,
,
所以
所以 为圆
为圆 的直径,即
的直径,即
设正方形 的边长为
的边长为
在
在
解得
所以
过点E作
由于
所以
因为
因为
因为
所以 的平面角
的平面角
在
因为
所以
在
所以
故二面角 的平面角的正切值为
的平面角的正切值为

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
 (III)求二面角
(III)求二面角 所在平面与圆
所在平面与圆 所在平面相交于
所在平面相交于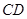 ,线段
,线段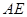 垂直于圆
垂直于圆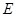 是圆
是圆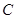 .
.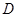 的点,
的点,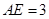 ,圆
,圆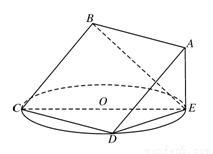
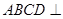 平面
平面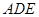 ;
;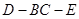 的平面角的正切值.
的平面角的正切值.