题目内容
【题目】已知函数
.
（I）求函数
在
上的最值；
（II）已知函数
，求证：
，
恒成立.
【答案】(I)
，
；(II)证明见解析.
【解析】
试题分析：(I)借助题设条件运用导数的知识求解；(II)借助题设构造函数运用导数的知识分析推证.
试题解析：
（I）
的定义域为
，............................1分
恒成立对
，............................2分
在
上递增，
，...............4分
（II）证明：令
；............................5分
在
上恒成立，............7分
在区间
上递减，............................................................8分
，......................................................10分
在区间上，
恒成立............................................12分
练习册系列答案
阅读快车系列答案
相关题目
【题目】某企业生产的一种产品的广告费用
(单位:万元)与销售额
(单位:万元)的统计数据如下表:
广告费用 |
|
|
|
|
|
销售额 |
|
|
|
|
|
（1）根据上述数据，求出销售额
（万元)关于广告费用
（万元)的线性回归方程；
（2）如果企业要求该产品的销售额不少于
万元，则投入的广告费用应不少于多少万元?
（参考数值： 
.
回归直线的斜率和截距的最小二乘法估计公式分别为：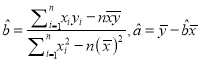 
）
