题目内容
设f（x）是定义在[a，b]上的函数，用分点T：a=x0＜x1＜…＜x i﹣1＜xi＜…xn=b
将区间[a，b]任意划分成n个小区间，
如果存在一个常数M＞0，使得
和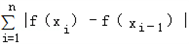
≤M（i=1，2，…，n）恒成立，
则称f（x）为[a，b]上的有界变差函数．
（1）函数f（x）=x2在[0，1]上是否为有界变差函数？请说明理由；
（2）设函数f（x）是[a，b]上的单调递减函数，证明：f（x）为[a，b]上的有界变差函数；
（3）若定义在[a，b]上的函数f（x）满足：存在常数k，使得对于任意的x1、x2∈[a，b]时，|f（x1）﹣f（x2）|≤k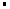
|x1﹣x2|．证明：f（x）为[a，b]上的有界变差函数．
解：（1）∵f（x）=x2在[0，1]上是增函数
∴对任意划分T，f（xn）＞f（x n﹣1）|f（xi）﹣f（x i﹣1）|
=f（x1）﹣f（x0）+…+f（xn）﹣f（xn﹣1）
=f（1）﹣f（0）=1
取常数M≥1，则和式
（i=1，2，3…n）恒成立
所以函数f（x）在[0，1]是有界变差函数
（2）∵函数f（x）是[a，b]上的单调递减函数任意的划分T，
a=x0＜x1＜…＜x i﹣1＜xi＜…＜xn=b
∴
=f（x0）-f（x1）+ f（x1）-f（x2）+...+f（x n-1）-f（xn）
=f（a）- f（b）
∴一定存在一个常数M＞0，使f（a）﹣f（b）≤M
故f（x）为[a，b]上有界变差函数
（3）∵|f（x1）﹣f（x2）|≤k
|x1﹣x2|
∴对任意的划分T，a=x0＜x1＜…＜x i﹣1＜x i＜…＜xn
=b
=
=k（b﹣a）
取常数M=k（b﹣a）f（x）为有界变差函数．
∴对任意划分T，f（xn）＞f（x n﹣1）|f（xi）﹣f（x i﹣1）|
=f（x1）﹣f（x0）+…+f（xn）﹣f（xn﹣1）
=f（1）﹣f（0）=1
取常数M≥1，则和式
（i=1，2，3…n）恒成立所以函数f（x）在[0，1]是有界变差函数
（2）∵函数f（x）是[a，b]上的单调递减函数任意的划分T，
a=x0＜x1＜…＜x i﹣1＜xi＜…＜xn=b
∴
=f（x0）-f（x1）+ f（x1）-f（x2）+...+f（x n-1）-f（xn）=f（a）- f（b）
∴一定存在一个常数M＞0，使f（a）﹣f（b）≤M
故f（x）为[a，b]上有界变差函数
（3）∵|f（x1）﹣f（x2）|≤k
|x1﹣x2|∴对任意的划分T，a=x0＜x1＜…＜x i﹣1＜x i＜…＜xn
=b
=
=k（b﹣a）取常数M=k（b﹣a）f（x）为有界变差函数．
练习册系列答案
相关题目
设f（x）是定义在R上的周期为3的周期函数，如图表示该函数在区间（-2，1]上的图象，则f（2013）+f（2014）=（ ）