题目内容
已知:在函数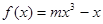 的图象上,以
的图象上,以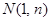 为切点的切线的倾斜角为
为切点的切线的倾斜角为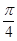 .
.
(Ⅰ)求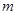 ,
,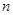 的值;
的值;
(Ⅱ)是否存在最小的正整数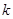 ,使得不等式
,使得不等式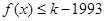 对于
对于 恒成立?如果存在,请求出最小的正整数
恒成立?如果存在,请求出最小的正整数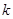 ;如果不存在,请说明理由;
;如果不存在,请说明理由;
(Ⅲ)求证: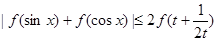 (
(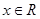 ,
,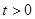 ).
).
【答案】
(Ⅰ)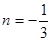 .
.
(Ⅱ)存在最小的正整数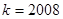 ,使得不等式
,使得不等式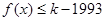 对于
对于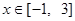 恒成立.
恒成立.
(Ⅲ)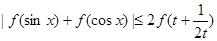 (
(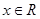 ,
,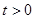 ).
).
【解析】
试题分析:(Ⅰ)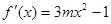 ,依题意,得
,依题意,得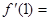
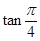 ,即
,即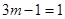 ,
,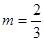 .
.
2分
∵ 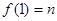 , ∴
, ∴ 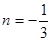 . 3分
. 3分
(Ⅱ)令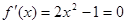 ,得
,得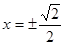 . 4分
. 4分
当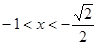 时,
时,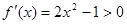 ;
;
当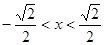 时,
时,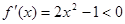 ;
;
当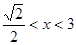 时,
时,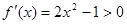 .
.
又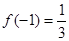 ,
,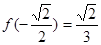 ,
,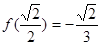 ,
,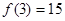 .
.
因此,当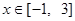 时,
时,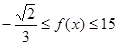 . 7分
. 7分
要使得不等式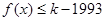 对于
对于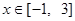 恒成立,则
恒成立,则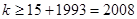 .
.
所以,存在最小的正整数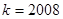 ,使得不等式
,使得不等式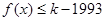 对于
对于
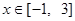 恒成立. 9分
恒成立. 9分
(Ⅲ)方法一: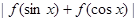
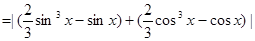
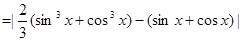
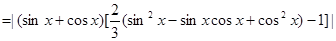
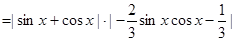
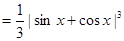
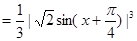
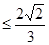 .
11分
.
11分
又∵ 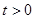 ,∴
,∴ 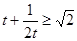 ,
,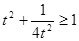 .
.
∴ 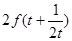
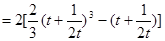

 .
13分
.
13分
综上可得,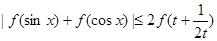 (
(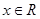 ,
,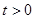 ).
14分
).
14分
方法二:由(Ⅱ)知,函数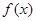 在 [-1,
在 [-1,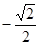 ]上是增函数;在[
]上是增函数;在[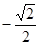 ,
,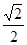 ]上是减函数;在[
]上是减函数;在[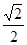 ,1]上是增函数.
,1]上是增函数.
又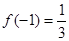 ,
,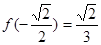 ,
,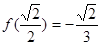 ,
,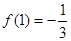 .
.
所以,当x∈[-1,1]时,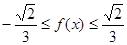 ,即
,即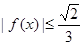 .
.
∵ 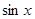 ,
,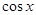 ∈[-1,1],∴
∈[-1,1],∴ 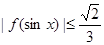 ,
,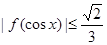 .
.
∴ 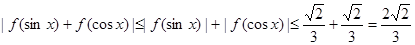 . 11分
. 11分
又∵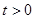 ,∴
,∴ 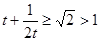 ,且函数
,且函数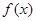 在
在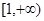 上是增函数.
上是增函数.
∴ 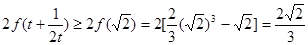 . 13分
. 13分
综上可得,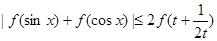 (
(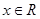 ,
,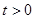 ).
14分
).
14分
考点:本题主要考查应用导数研究函数的单调性及极值,均值定理的应用,三角函数恒等变换。
点评:难题,本题综合性较强,对复杂式子的变形能力要求较高。不等式的证明中,灵活运用不等式的性质是一个关键点。

练习册系列答案
相关题目
 以
以 为切点的切线的倾斜角为
为切点的切线的倾斜角为
 的值;
的值; ,使得不等式
,使得不等式 恒成立?如果存在,请求出最小的正整数
恒成立?如果存在,请求出最小的正整数