题目内容
如图在四棱锥P-ABCD中侧面PAD⊥底面ABCD,侧棱PA⊥PD,底面ABCD为直角梯形.其中BC∥AD,∠BAD=90°,AD=3BC,O是AD上一点
①若CD∥平面PBO 试指出O的位置并说明理由
②求证平面PAB⊥平面PCD
③若PD=BC=1,AB=2
,求P-ABCD的体积.
①若CD∥平面PBO 试指出O的位置并说明理由
②求证平面PAB⊥平面PCD
③若PD=BC=1,AB=2
| 2 |

①因为CD∥平面PBO,CD?平面ABCD,且平面ABCD∩平面PBO=BO,
所以BO∥CD
又BC∥AD,
所以四边形BCDO为平行四边形,则BC=DO,
而AD=3BC,故点O的位置满足AO=2OD.
②证明:因为侧面PAD⊥底面ABCD,AB?底面ABCD,且AB⊥交线AD,
所以AB⊥平面PAD,则AB⊥PD又PA⊥PD,
且PA?平面PAB,AB?平面PAB,AB∩PA=A,
所以PD⊥平面PAB,PD?平面PCD,
所以:平面PAB⊥平面PCD;
③过P作PE⊥AD,
∵侧面PAD⊥底面ABCD,侧面PAD∩底面ABCD=AD,
∴PE⊥底面ABCD,
∵PD=1,AD=3BC,棱PA⊥PD,
∴PA=2
∴PE=
∵AB=2
,∠BAD=90°
∴P-ABCD的体积为
•
•(1+3)•2
•
=
.
所以BO∥CD
又BC∥AD,
所以四边形BCDO为平行四边形,则BC=DO,
而AD=3BC,故点O的位置满足AO=2OD.
②证明:因为侧面PAD⊥底面ABCD,AB?底面ABCD,且AB⊥交线AD,
所以AB⊥平面PAD,则AB⊥PD又PA⊥PD,
且PA?平面PAB,AB?平面PAB,AB∩PA=A,
所以PD⊥平面PAB,PD?平面PCD,
所以:平面PAB⊥平面PCD;
③过P作PE⊥AD,
∵侧面PAD⊥底面ABCD,侧面PAD∩底面ABCD=AD,
∴PE⊥底面ABCD,
∵PD=1,AD=3BC,棱PA⊥PD,
∴PA=2
| 2 |
∴PE=
2
| ||
| 3 |
∵AB=2
| 2 |
∴P-ABCD的体积为
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
2
| ||
| 3 |
| 16 |
| 9 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
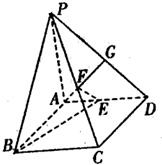 如图在四棱锥P-ABCD中,底ABCD是矩形,PA⊥面ABCD,AP=AB=2,BC=2
如图在四棱锥P-ABCD中,底ABCD是矩形,PA⊥面ABCD,AP=AB=2,BC=2 如图在四棱锥P-ABCD中,PA⊥底面ABCD,∠DAB为直角,AB∥CD,AD=CD=2AB,E、F分别为PC、CD的中点;PA=kAB(k>0),且二面角E-BD-C的平面角大于30°,则k的取值范围是( )
如图在四棱锥P-ABCD中,PA⊥底面ABCD,∠DAB为直角,AB∥CD,AD=CD=2AB,E、F分别为PC、CD的中点;PA=kAB(k>0),且二面角E-BD-C的平面角大于30°,则k的取值范围是( ) 如图在四棱锥P-ABCD中侧面PAD⊥底面ABCD,侧棱PA⊥PD,底面ABCD为直角梯形.其中BC∥AD,∠BAD=90°,AD=3BC,O是AD上一点
如图在四棱锥P-ABCD中侧面PAD⊥底面ABCD,侧棱PA⊥PD,底面ABCD为直角梯形.其中BC∥AD,∠BAD=90°,AD=3BC,O是AD上一点 如图在四棱锥P-ABCD中,侧棱PD⊥平面ABCD,M,N分别是AB,PC的中点,底面ABCD是菱形,
如图在四棱锥P-ABCD中,侧棱PD⊥平面ABCD,M,N分别是AB,PC的中点,底面ABCD是菱形, 如图在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥底面ABCD,垂足为点A,PA=AB=1,点M,N分别是PD,PB的中点.
如图在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥底面ABCD,垂足为点A,PA=AB=1,点M,N分别是PD,PB的中点.