题目内容
已知函数f(x)=2sin(ωx+φ)(ω>0,-
<φ<
)的图象如图所示,直线x=
,x=
是其两条对称轴.
(1)求函数f(x)的解析式;
(2)若f(a)=
,且
<α<
,求f(
+α)的值.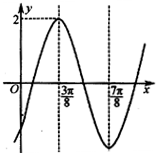
| π |
| 2 |
| π |
| 2 |
| 3π |
| 8 |
| 7π |
| 8 |
(1)求函数f(x)的解析式;
(2)若f(a)=
| 6 |
| 5 |
| π |
| 8 |
| 3π |
| 8 |
| π |
| 8 |

(本题满分14分)
(1)由题意,
=
-
=
,∴T=π.
又ω>0,故ω=2,∴f(x)=2sin(2x+φ).(2分)
由f(
)=2sin(
+φ)=2,解得φ=2kπ-
(k∈Z).
又-
<φ<
,∴φ=-
,∴f(x)=2sin(2x-
).(5分)
由2kπ-
≤2x-
≤2kπ+
(k∈Z),知kπ-
≤x≤kπ+
(k∈Z),
∴函数f(x)的单调增区间为[kπ-
,kπ+
](k∈Z).(7分)
(2)解法1:依题意得2sin(2α-
)=
,即sin(2α-
)=
,(8分)
∵
<α<
,∴0<2α-
<
.
∴cos(2α-
)=
,(10分)
f(
+α)=2sin[(2α-
)+
].
∵sin[(2α-
)+
]=sin(2α-
)cos
+cos(2α-
)sin
=
(
+
)=
,
∴f(
+α)=
.(14分)
解法2:依题意得sin(2α-
)=
,得sin2α-cos2α=
,①(9分)
∵
<α<
,∴0<2α-
<
,
∴cos(α-
)=
,(11分)
由cos(2α-
)=
得sin2α+cos2α=
.②
①+②得2sin2α=
,
∴f(
+α)=
.(14分)
(1)由题意,
| T |
| 2 |
| 7π |
| 8 |
| 3π |
| 8 |
| π |
| 2 |
又ω>0,故ω=2,∴f(x)=2sin(2x+φ).(2分)
由f(
| 3π |
| 8 |
| 3π |
| 4 |
| π |
| 4 |
又-
| π |
| 2 |
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
由2kπ-
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
| π |
| 8 |
| 3π |
| 8 |
∴函数f(x)的单调增区间为[kπ-
| π |
| 8 |
| 3π |
| 8 |
(2)解法1:依题意得2sin(2α-
| π |
| 4 |
| 6 |
| 5 |
| π |
| 4 |
| 3 |
| 5 |
∵
| π |
| 8 |
| 3π |
| 8 |
| π |
| 4 |
| π |
| 2 |
∴cos(2α-
| π |
| 4 |
| 4 |
| 5 |
f(
| π |
| 8 |
| π |
| 4 |
| π |
| 4 |
∵sin[(2α-
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| ||
| 2 |
| 3 |
| 5 |
| 4 |
| 5 |
7
| ||
| 10 |
∴f(
| π |
| 8 |
7
| ||
| 5 |
解法2:依题意得sin(2α-
| π |
| 4 |
| 3 |
| 5 |
3
| ||
| 5 |
∵
| π |
| 8 |
| 3π |
| 8 |
| π |
| 4 |
| π |
| 2 |
∴cos(α-
| π |
| 4 |
| 4 |
| 5 |
由cos(2α-
| π |
| 4 |
| 4 |
| 5 |
4
| ||
| 5 |
①+②得2sin2α=
7
| ||
| 5 |
∴f(
| π |
| 8 |
7
| ||
| 5 |

练习册系列答案
相关题目