题目内容
已知函数![]() (其中常数
(其中常数![]() ).
).
(1) 当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(2) 若![]() 在
在 ![]() 处取得极值,且在
处取得极值,且在![]() 上的最大值为
上的最大值为![]() ,求
,求![]() 的值.
的值.
【解析】解:(1)当![]() 时,因为
时,因为![]() 所以
所以![]() (1分)
(1分)
![]()
![]()
令![]() ,解得
,解得![]() (2分)
(2分)
当![]() 时,
时,![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递增;
上单调递增;
所以![]() 的单调递增区间为
的单调递增区间为![]() ,
,![]() ,单调递减区间为
,单调递减区间为![]() (5分)
(5分)
(2)因为![]()
令![]() ,
,![]() (6分)
(6分)
因为![]() 在
在![]() 处取得极值,所以
处取得极值,所以![]()
当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
所以![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,令
,令![]() ,解得
,解得![]() (8分)
(8分)
当![]() ,
,![]()
当![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,![]() 上单调递减,
上单调递减,![]() 上单调递增
上单调递增
所以最大值1可能在![]() 或
或![]() 处取得
处取得
而![]()
所以![]() ,解得
,解得![]() (10分)
(10分)
当![]() 时,
时,![]() 在区间
在区间![]() 上单调递增,
上单调递增,![]() 上单调递减,
上单调递减,![]() 上单调递增
上单调递增
所以最大值1可能在![]() 或
或![]() 处取得
处取得
而![]()
所以![]() ,
,
解得![]() ,与
,与![]() 矛盾
矛盾
当![]() 时,
时,![]() 在区间
在区间![]() 上单调递增,在
上单调递增,在![]() 单调递减,
单调递减,
所以最大值1可能在![]() 处取得,而
处取得,而![]() ,矛盾. (13分)
,矛盾. (13分)
综上所述,![]() 或
或![]() . (14分)
. (14分)

练习册系列答案
相关题目
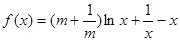 ,其中常数
,其中常数 .
.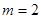 时,求函数
时,求函数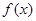 的极大值;
的极大值;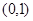 上的单调性;
上的单调性;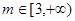 时,曲线
时,曲线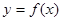 上总存在相异两点
上总存在相异两点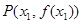 ,
,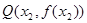 ,使得曲线
,使得曲线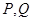 处的切线互相平行,求
处的切线互相平行,求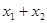 的取值范围.
的取值范围.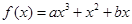 (其中常数a,b∈R),
(其中常数a,b∈R),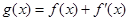 是奇函数.
是奇函数.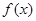 的表达式;
的表达式; 的单调性,并求
的单调性,并求 其中常数
其中常数
 时,求函数
时,求函数 的单调递增区间;
的单调递增区间; 时,给出两类直线:
时,给出两类直线: 与
与 ,其中
,其中 为常数,判断这两类直线中是否存在
为常数,判断这两类直线中是否存在 的切线,若存在,求出相应的
的切线,若存在,求出相应的 或
或 的值,若不存在,说明理由.
的值,若不存在,说明理由. 上的函数
上的函数 在点
在点 处的切线方程为
处的切线方程为 ,当
,当 若
若 在
在 为函数
为函数 (其中常数a,b∈R),
(其中常数a,b∈R), 是奇函数.
是奇函数. 的表达式;(2)讨论
的表达式;(2)讨论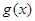 的单调性,并求
的单调性,并求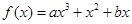 (其中常数a,b∈R),
(其中常数a,b∈R),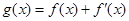 是奇函数.
是奇函数. 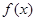 的表达式;
的表达式; 的单调性,并求
的单调性,并求