题目内容
设方程 的实根为
的实根为 ,方程
,方程 的实根为
的实根为 ,函数
,函数 则
则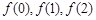 的大小关系是( )
的大小关系是( )
A. | B. |
C. | D. |
B
解析试题分析:根据题意可知方程 的实根为
的实根为 ,方程
,方程 的实根为
的实根为 ,则可以作图函数y=2x,与y=log2x与直线y=-x-2的交点的横坐标即为根的大小,可知一个小于-2,一个大于零小于1,且关于直线y=x对称,因此可知两个横坐标的和为-2,那么在函数
,则可以作图函数y=2x,与y=log2x与直线y=-x-2的交点的横坐标即为根的大小,可知一个小于-2,一个大于零小于1,且关于直线y=x对称,因此可知两个横坐标的和为-2,那么在函数 中,可知二次函数对称轴
中,可知二次函数对称轴 =1,同时结合开口方向和定义域与对称轴的关系可知,
=1,同时结合开口方向和定义域与对称轴的关系可知, ,选B。
,选B。
考点:本题主要是考查函数与方程的思想的运用。
点评:解决该试题的关键是根据函数y=2x,与y=log2x与直线y=-x-2的交点得到根 和
和 ,进而分析得到二次函数中函数值大小的比较。
,进而分析得到二次函数中函数值大小的比较。

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
函数 的最大值为( )
的最大值为( )
A. | B. | C. | D. |
方程 的实数解落在的区间是
的实数解落在的区间是
A. | B. | C. | D. |
下列函数中,在区间 上为增函数的是
上为增函数的是
A. | B. |
C.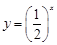 | D.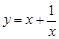 |
已知函数 则函数零点个数为 ( )
则函数零点个数为 ( )
| A.1 | B.2 | C.3 | D.4 |
已知定义在R上的奇函数
 ,满足
,满足 ,且在区间[0,2]上是增函数,则( )
,且在区间[0,2]上是增函数,则( )
A. | B. |
C. | D. |
设偶函数 的定义域为R,当
的定义域为R,当
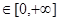 时,
时, 是增函数,则
是增函数,则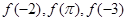 的大小关系是( )
的大小关系是( )
A. | B. |
C. | D. |
已知函数 有2个不同的零点
有2个不同的零点 、
、 ,则
,则
A. | B.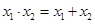 |
C. | D. |
 与
与 的图象如所示,则函数
的图象如所示,则函数 的图象可能为( )
的图象可能为( )
