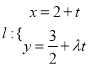题目内容
【题目】已知椭圆![]() 的离心率
的离心率![]() ,直线
,直线![]() 与圆
与圆![]() 相切.
相切.
(1)求椭圆的方程;
(2)已知定点![]() ,若直线
,若直线![]() 与椭圆相交于
与椭圆相交于![]() 两点,试判断是否存在实数
两点,试判断是否存在实数![]() ,使得以
,使得以![]() 为直径的圆过定点
为直径的圆过定点![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() ;(2)存在实数
;(2)存在实数![]() 使得以
使得以![]() 为直径的圆过定点
为直径的圆过定点![]() .
.
【解析】试题分析: (1)圆心到切线距离等于半径得![]() ,即
,即![]() ,再根据离心率
,再根据离心率![]() ,解得
,解得![]() ,(2)由以
,(2)由以![]() 为直径的圆过点
为直径的圆过点![]() ,得
,得![]() ,设坐标转化条件得
,设坐标转化条件得![]() ,将直线方程与椭圆方程联立,利用韦达定理得
,将直线方程与椭圆方程联立,利用韦达定理得![]() ,
,![]() ,代入条件并化简得
,代入条件并化简得![]() .
.
试题解析:(1)因为直线![]() :
:![]() 与圆
与圆![]() 相切,
相切,
∴![]() ,
,
∴![]() ,
,
∵椭圆的离心率![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴所求椭圆的方程是![]() .
.
(2)直线![]() 代入椭圆方程,消去
代入椭圆方程,消去![]() 可得:
可得:![]()
∴![]() ,∴
,∴![]() 或
或![]() ,
,
设![]() ,则有
,则有![]() ,
,![]() ,
,
若以![]() 为直径的圆过点
为直径的圆过点![]() ,则
,则![]() ,
,
∵![]() ,
,![]() ,
,
∴![]()
∴![]()
∴![]() ,
,
解得![]() ,
,
所以存在实数![]() 使得以
使得以![]() 为直径的圆过定点
为直径的圆过定点![]() .
.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
【题目】某班主任对全班50名学生的学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
积极参加班级工作 | 不太主动参加班级工作 | 合计 | |
学习积极性一般 | 6 | 19 | 25 |
合计 | 24 | 26 | 50 |
(1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(2)判断是否有![]() 的把握认为学生的学习积极性与对待班级工作的态度有关系?
的把握认为学生的学习积极性与对待班级工作的态度有关系?
附:  , n=a+b+c+d.
, n=a+b+c+d.
P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 6.635 | 10.828 |