题目内容
已知函数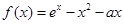 ,如果函数
,如果函数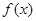 恰有两个不同的极值点
恰有两个不同的极值点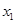 ,
, ,且
,且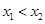 .
.
(Ⅰ)证明: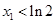 ;
;
(Ⅱ)求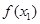 的最小值,并指出此时
的最小值,并指出此时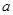 的值.
的值.
【答案】
(Ⅰ)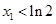 ;(Ⅱ)
;(Ⅱ)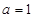 .
.
【解析】
试题分析:(Ⅰ)因为 函数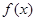 恰有两个不同的极值点
恰有两个不同的极值点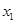 ,
,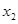 ,即
,即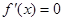 有两个零点
有两个零点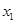 ,
,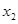 ,则
,则
方程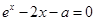 有两个不同的零点
有两个不同的零点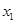 ,
,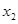 ,构造函数
,构造函数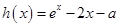 ,求导
,求导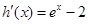 ,
,
当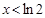 时,
时,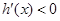 ,
,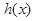 是减函数;当
是减函数;当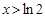 时,
时,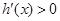 ,
,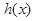 是增函数,所以
是增函数,所以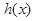 在
在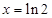 时取得最小值.∴
时取得最小值.∴ 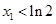 .(Ⅱ)由(Ⅰ)知
.(Ⅱ)由(Ⅰ)知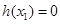 ,即
,即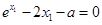 ,所以
,所以 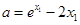 ,
,
于是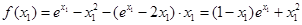 ,所以
,所以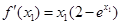 ,
,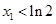 ,所以
,所以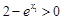 .所以 当
.所以 当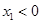 时,
时,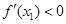 ,
,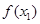 是减函数;当
是减函数;当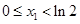 时,
时,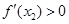 ,
,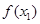 是增函数,所以
是增函数,所以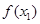 在
在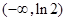 上的最小值为
上的最小值为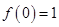 ,此时
,此时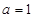 .
.
试题解析:(Ⅰ)∵ 函数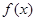 恰有两个不同的极值点
恰有两个不同的极值点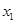 ,
,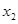 ,即
,即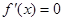 有两个零点
有两个零点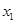 ,
,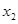
∴ 方程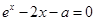 有两个不同的零点
有两个不同的零点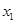 ,
,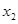
令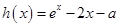 .
.
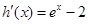 ,
,
当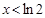 时,
时,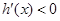 ,
,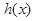 是减函数;
是减函数;
当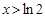 时,
时,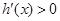 ,
,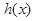 是增函数,
是增函数,
∴ 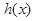 在
在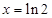 时取得最小值.
时取得最小值.
∴ 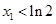 .
.
(Ⅱ)∵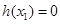 ,即
,即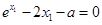 ,
,
∴ 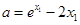
于是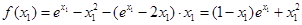 ,
,
∴ 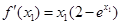
∵ 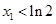 ,
,
∴ 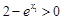 .
.
∴ 当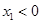 时,
时,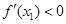 ,
,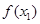 是减函数;
是减函数;
当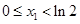 时,
时,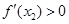 ,
,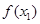 是增函数
是增函数
∴ 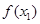 在
在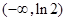 上的最小值为
上的最小值为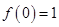 ,此时
,此时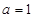 .
.
考点:1.函数中证明问题;3.函数与不等式的综合应用.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
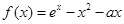 ,如果函数
,如果函数 恰有两个不同的极值点
恰有两个不同的极值点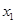 ,
,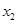 ,且
,且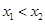 .
.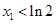 ;(Ⅱ)求
;(Ⅱ)求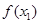 的最小值,并指出此时
的最小值,并指出此时 的值.
的值. 和
和 .其中
.其中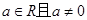 .
. 与
与 的图像的一个公共点恰好在x轴上,求
的图像的一个公共点恰好在x轴上,求 的值;w
的值;w  和
和 是方程
是方程 的两根,且满足
的两根,且满足 ,
, 时,
时, .
.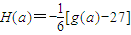 ,数列{an}满足an+1=H(an)(n∈N*),且a1∈(0,1),试判断an+1与an的大小,并证明之.
,数列{an}满足an+1=H(an)(n∈N*),且a1∈(0,1),试判断an+1与an的大小,并证明之.