Question

【题目】A已知直线的参数方程为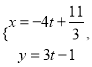（为参数），在直角坐标系中，以为极点， 轴正半轴为极轴建立极坐标系，圆的方程为

(1)求圆的圆心的极坐标；

(2)判断直线与圆的位置关系.

已知不等式的解集为

（1）求实数的值；

（2）若不等式对恒成立，求实数的取值范围.

Answer 1

【答案】（1）直角坐标为,极坐标为（2）见解析.

（1）.（2）.

【解析】试题分析：A（1）根据极坐标与普通方程的转化公式，极坐标方程化为普通方程；（2）先利用消参的方法得一般方程，再利用圆心到直线距离判定直线与圆位置关系.B（1）通过平方的方式解绝对值不等式（2）去绝对号转化为分段函数，求值域.

试题解析： （1） , 的直角坐标为,极坐标为

（2）直线的参数方程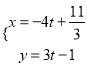,( 为参数)化为普通方程得

由（1）知,圆的圆心为半径为,且到直线的距离直线与圆相切.

（1）由得,即

即

（2）设,

则