题目内容
植树节来临,某学校数学活动小组在坐标纸上为学校的一块空地设计植树方案如下:第k棵树种植在P(xk,yk)处,其中x1=1,y1=1,当k≥2时,
|
分析:由题意可知,数列{xn}为1,2,3,4,5,1,2,3,4,5,1,2,3,4,5,…;数列{yn}为1,1,1,1,1,2,2,2,2,2,3,3,3,3,3,4,4,4,4,4,…由此入手能够得到第2011棵树种植点的坐标.
解答:解:∵T(
) -T(
)成的数列为1,0,0,0,0,1,0,0,0,0,1,0,0,0,0,1…,k=1,2,3,4,5,…一一代入计算得数列{xn}为1,2,3,4,5,1,2,3,4,5,1,2,3,4,5,…即{xn}是以5为周期的周期数列,从而有x5n+1=1,x5n+2=2,x5n+3=3,x5n+4=4,x5n=5.n∈N*.
数列{yn}为1,1,1,1,1,2,2,2,2,2,3,3,3,3,3,4,4,4,4,4,…即yn的重复规律是y 5n+k=n,0≤k<5.∴由题意可知第2011棵树种植点的坐标应为(1,202).
故答案为(1,202)
| k-1 |
| 5 |
| k-2 |
| 5 |
数列{yn}为1,1,1,1,1,2,2,2,2,2,3,3,3,3,3,4,4,4,4,4,…即yn的重复规律是y 5n+k=n,0≤k<5.∴由题意可知第2011棵树种植点的坐标应为(1,202).
故答案为(1,202)
点评:本题考查数列的性质和应用,解题的关键是由特殊到一般,从而得出数列为周期数列.解题时要注意创新题的灵活运用.

练习册系列答案
相关题目
 处,其中
处,其中 ,当
,当 时,
时,
 表示非负实数
表示非负实数 的整数部分,如
的整数部分,如 .按此方案,第2
.按此方案,第2 011棵树种植点的坐标是 .
011棵树种植点的坐标是 .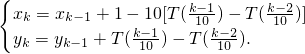 .其中T(a)表示非负实数a的整数部分,如T(2.7)=2,T(0.3)=0.按此方案,第2011棵树种植点的坐标是________.
.其中T(a)表示非负实数a的整数部分,如T(2.7)=2,T(0.3)=0.按此方案,第2011棵树种植点的坐标是________. .其中T(a)表示非负实数a的整数部分,如T(2.7)=2,T(0.3)=0.按此方案,第2011棵树种植点的坐标是 .
.其中T(a)表示非负实数a的整数部分,如T(2.7)=2,T(0.3)=0.按此方案,第2011棵树种植点的坐标是 .