题目内容
已知f(x)=2mx+m2+2,m≠0,m∈R,x∈R.若|x1|+|x2|=1,则
的取值范围是
| f(x1) |
| f(x2) |
[1-
,2+
]
| ||
| 2 |
| 2 |
[1-
,2+
]
.
| ||
| 2 |
| 2 |
分析:(i)法一:目标函数法:①分类讨论去绝对值找x1,x2的关系.②将
化为一个变量的函数g(x2).
(ii)法二:数形结合:①“数”难时,要考虑“形”.②C:|x1|+|x2|=1为正方形.③“分式”联想到斜率.
| f(x1) |
| f(x2) |
(ii)法二:数形结合:①“数”难时,要考虑“形”.②C:|x1|+|x2|=1为正方形.③“分式”联想到斜率.
解答:解: 解法一:
解法一:
先考虑0≤x1≤1,0≤x2≤1的情形,
则x1+x2=1
=
=
=-1+
当m>0,令函数g(x)=-1+
,x∈[0,1],
由单调性可得:g(1)≤g(x)≤g(0).其中,g(1)=1-
≥2-
,g(0)=1+
≤1+
当m<0,同理.x1、x2在其他范围同理.
综上可得[1-
,2+
].
解法二:
=
=
,∴
为点P(-
,-
)与点Q(x2,x1)连线的斜率.P点在直线y=x(|x|≥
)上.
由图可得直线PQ斜率的范围,即
的范围.
 解法一:
解法一:先考虑0≤x1≤1,0≤x2≤1的情形,
则x1+x2=1
| f(x1) |
| f(x2) |
| 2mx1+m2+2 |
| 2mx2+m2+2 |
| 2m(1-x2)+m2+2 |
| 2mx2+m2+2 |
m+1+
| ||||
x2+
|
当m>0,令函数g(x)=-1+
m+1+
| ||||
x+
|
由单调性可得:g(1)≤g(x)≤g(0).其中,g(1)=1-
| 2 | ||
m+
|
| 2 |
| 2 | ||
m+
|
| ||
| 2 |
当m<0,同理.x1、x2在其他范围同理.
综上可得[1-
| ||
| 2 |
| 2 |
解法二:
| f(x1) |
| f(x2) |
| 2mx1+m2+2 |
| 2mx2+m2+2 |
x1+
| ||
x2+
|
| f(x1) |
| f(x2) |
| m2+2 |
| 2m |
| m2+2 |
| 2m |
| 2 |
由图可得直线PQ斜率的范围,即
| f(x1) |
| f(x2) |
点评:熟练掌握分类讨论、数形结合的思想方法、函数的单调性、直线的斜率公式及意义是解题的关键.

练习册系列答案
相关题目
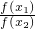 的取值范围是________.
的取值范围是________.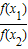 的取值范围是 .
的取值范围是 .