题目内容

设数列{an}的前n项和为Sn，已知ban-2n=(b-1)Sn..

（Ⅰ）证明：当b=2时，{an-n·2n-1}是等比数列；

（Ⅱ）求{an}的通项公式.

解：由题意知，a1=2，且

         ban-2n=(b-1)Sn，

         ban+1-2n+1=(b-1)Sn+1，

 两式相减得　b(an+1-an)-2n=(b-1)an+1,

即　　　　an+1=ban+2n ,                                       ①

(Ⅰ)当b=2时，由①知，an+1=2an+2n,

于是　　　　　　　　an+1-(n+1)·2n=2an+2n-(n+1)·2n

                                                =2(an-n·2n-1)，

又所以{an-n·2n-1}是首项为1，公比为2的等比数列，

（Ⅱ）当b=2时，由（Ⅰ）知，即

　　　当时，由①得

　　　

　　　　　　　　　　　＝

　　　　　　　　　　　

因此　　　

　　　　　　　　　　　　　

得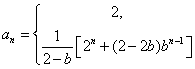　　　　　　　

练习册系列答案
相关题目
设数列{an}的前n项的和为Sn，且Sn=3n+1．
（1）求数列{an}的通项公式；
（2）设bn=an（2n-1），求数列{bn}的前n项的和．
设数列an的前n项的和为Sn，a1=
3
2
，Sn=2an+1-3．
（1）求a2，a3；
（2）求数列an的通项公式；
（3）设bn=(2log
3
2
an+1)•an，求数列bn的前n项的和Tn．
设数列{an}的前n项和Sn=2an+
3
2
×（-1）n-
1
2
，n∈N*．
（Ⅰ）求an和an-1的关系式；
（Ⅱ）求数列{an}的通项公式；
（Ⅲ）证明：
1
S1
+
1
S2
+…+
1
Sn
＜
10
9
，n∈N*．
不等式组
x≥0
y≥0
nx+y≤4n
所表示的平面区域为Dn，若Dn内的整点（整点即横坐标和纵坐标均为整数的点）个数为an（n∈N*）
（1）写出an+1与an的关系（只需给出结果，不需要过程），
（2）求数列{an}的通项公式；
（3）设数列an的前n项和为Sn且Tn=
Sn
5•2n
，若对一切的正整数n，总有Tn≤m成立，求m的范围．
（2013•郑州一模）设数列{an}的前n项和Sn=2n-1，则
S4
a3
的值为（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网