题目内容
已知数列{an}满足:a1=3,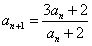 ,n∈N*,记
,n∈N*,记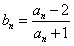 。
。
(I)求证:数列{bn}是等比数列;
(Ⅱ)若an≤t·4n对任意n∈N*恒成立,求t的取值范围;
(Ⅲ)记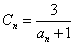 ,求证:C1·C2·…· Cn>
,求证:C1·C2·…· Cn>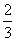 。
。
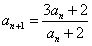 ,n∈N*,记
,n∈N*,记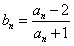 。
。(I)求证:数列{bn}是等比数列;
(Ⅱ)若an≤t·4n对任意n∈N*恒成立,求t的取值范围;
(Ⅲ)记
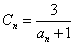 ,求证:C1·C2·…· Cn>
,求证:C1·C2·…· Cn>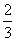 。
。(Ⅰ)证明:由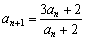 ,得
,得
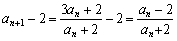 , ①
, ①
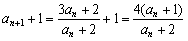 , ②
, ②
∴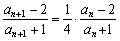 ,即
,即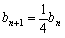 ,且
,且 ,
,
∴数列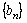 是首项为
是首项为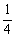 ,公比为
,公比为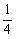 的等比数列.
的等比数列.
(Ⅱ)解:由(Ⅰ)知,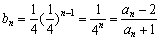 ,
,
∴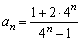 ,
,
由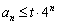 得
得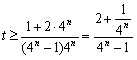 ,
,
易知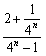 是关于n的减函数,
是关于n的减函数,
∴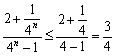 ,解得:
,解得: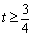 。
。
(Ⅲ)解:由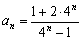 ,得
,得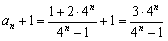 ,
,
∴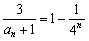 ,
,
∴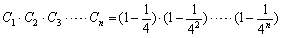 ,
,
下面用数学归纳法证明不等式:
若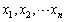 为正数,则
为正数,则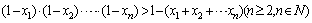 (*)
(*)
1o当n=2时,∵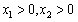 ,
,
∴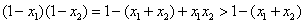 ;
;
2o假设当n=k(k≥2)时,不等式成立,即若x1,x2,……,xk为正数,
则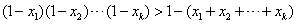 ,
,
那么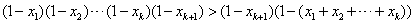
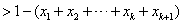 ,
,
这就是说当n=k+1时不等式成立。
根据不等式(*)得:
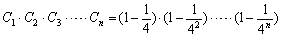
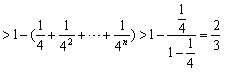 ,
,
∴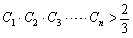 。
。
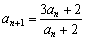 ,得
,得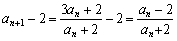 , ①
, ①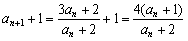 , ②
, ②∴
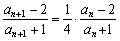 ,即
,即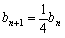 ,且
,且 ,
,∴数列
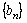 是首项为
是首项为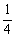 ,公比为
,公比为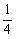 的等比数列.
的等比数列. (Ⅱ)解:由(Ⅰ)知,
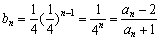 ,
,∴
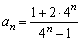 ,
,由
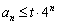 得
得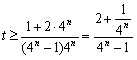 ,
,易知
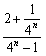 是关于n的减函数,
是关于n的减函数,∴
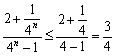 ,解得:
,解得: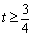 。
。(Ⅲ)解:由
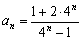 ,得
,得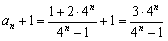 ,
,∴
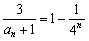 ,
,∴
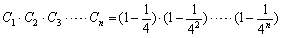 ,
,下面用数学归纳法证明不等式:
若
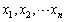 为正数,则
为正数,则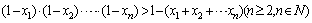 (*)
(*)1o当n=2时,∵
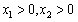 ,
,∴
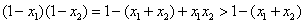 ;
;2o假设当n=k(k≥2)时,不等式成立,即若x1,x2,……,xk为正数,
则
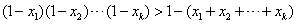 ,
,那么
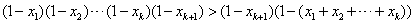
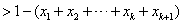 ,
,这就是说当n=k+1时不等式成立。
根据不等式(*)得:
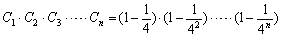
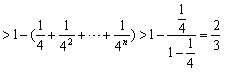 ,
,∴
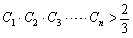 。
。
练习册系列答案
相关题目