题目内容
已知向量 若点A、B、C能构成三角形,则实数
若点A、B、C能构成三角形,则实数 应满足的条件是( )
应满足的条件是( )
A. B.
B. C.
C. D.
D.
C
解析试题分析:解:若点A、B、C不能构成三角形,则只能三点共线.∵ =(2,-1)-(1,-3)=(1,2),
=(2,-1)-(1,-3)=(1,2), =(m+1,m-2)-(1,-3)=(m,m+1).假设A、B、C三点共线,则1×(m+1)-2m=0,即m=1.∴若A、B、C三点能构成三角形,则m≠1.故选C
=(m+1,m-2)-(1,-3)=(m,m+1).假设A、B、C三点共线,则1×(m+1)-2m=0,即m=1.∴若A、B、C三点能构成三角形,则m≠1.故选C
考点:向量
点评:向量是数形结合的典型例子,向量的加减运算是用向量解决问题的基础,要学好运算,才能用向量解决立体几何问题,三角函数问题,好多问题都是以向量为载体的.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
在平面直角坐标系 中,已知点
中,已知点 ,若
,若 ,则实数
,则实数 的值为( )
的值为( )
A. | B. | C. | D. |
已知向量a=(2,1)b=(3,﹣1)向量a与b的夹角为 ,则
,则 =( )
=( )
| A.30° | B.45° | C.60° | D.90° |
下列命题正确的是( )
A.若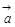 · ·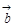 = =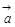 · ·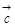 ,则 ,则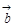 = =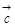 | B.若 ,则 ,则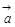 · ·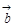 ="0" ="0" |
C.若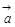 // //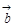 , ,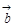 // //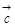 ,则 ,则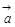 // //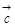 | D. |
如图,平行四边形ABCD的对角线交点是O,则下列等式成立的是( )
A. |
B. |
C. |
D. |
已知 ,
, ,则
,则 ( )
( )
A. | B. | C. | D. |
下列各组向量不平行的是( )
A. | B. |
C. | D. |
已知向量 ,
, ,若
,若 ,则
,则 =( )
=( )
| A.-4 | B.-3 | C.-2 | D.-1 |
 ,
, 为平面内一组基向量,
为平面内一组基向量, 为平面内任意一点,
为平面内任意一点,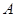 的对称点为
的对称点为 ,
, 的对称点为
的对称点为 ,则
,则 可以表示为( )
可以表示为( ) B.
B. C.
C. D.
D.