题目内容
已知函数f(x)=blnx,g(x)=ax2-x(a∈R).
(1)若曲线f(x)与g(x)在公共点A(1,0)处有相同的切线,求实数a、b的值;
(2)当b=1时,若曲线f(x)与g(x)在公共点P处有相同的切线,求证:点P唯一;
(3)若a>0,b=1,且曲线f(x)与g(x)总存在公切线,求正实数a的最小值.
解:(1)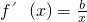 ,g'(x)=2ax-1.
,g'(x)=2ax-1.
∵曲线f(x)与g(x)在公共点A(1,0)处有相同的切线,
∴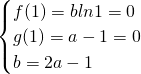 ,解得,
,解得,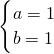 .
.
(2)设P(x0,y0),则由题设有 …①,
…①,
又在点P有共同的切线,∴ ,
,
代入①得 ,
,
设 ,则
,则 ,则h′(x)>0,
,则h′(x)>0,
∴h(x)在(0,+∞)上单调递增,所以 h(x)=0最多只有1个实根,
从而,结合(1)可知,满足题设的点P只能是P(1,0).
(3)当a>0,b=1时,f(x)=lnx,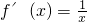 ,
,
曲线f(x)在点(t,lnt)处的切线方程为 ,即
,即 .
.
由 ,得
,得  .
.
∵曲线f(x)与g(x)总存在公切线,∴关于t(t>0)的方程 ,
,
即 (*)总有解.
(*)总有解.
若t>e,则1-lnt<0,而 ,显然(*)不成立,所以 0<t<e,
,显然(*)不成立,所以 0<t<e,
从而,方程(*)可化为 .
.
令 (0<t<e),则
(0<t<e),则 .
.
∴当0<t<1时,h'(t)<0;当1<t<e时,h'(t)>0,即 h(t)在(0,1)上单调递减,在(1,e)上单调递增.
∴h(t)在(0,e)上的最小值为h(1)=4,
所以,要使方程(*)有解,只须4a≥4,即a≥1.
所以正实数a的最小值为1.
分析:(1)因为曲线f(x)与g(x)在公共点A(1,0)处有相同的切线,所以 ,解出即可;
,解出即可;
(2)设P(x0,y0),由题设得f(x0)=g(x0),f′(x0)=g(x0),转化为关于x0的方程只有一解,进而构造函数转化为函数只有一个零点,利用导数即可证明;
(3)设曲线f(x)在点(t,lnt)处的切线方程为 ,则只需使该切线与g(x)相切即可,也即方程组
,则只需使该切线与g(x)相切即可,也即方程组 只有一解即可,所以消y后△=0,问题转化关于t的方程总有解,分情况借助导数进行讨论即可求得a值;
只有一解即可,所以消y后△=0,问题转化关于t的方程总有解,分情况借助导数进行讨论即可求得a值;
点评:本题考查利用导数研究曲线上某点切线方程问题,考查学生综合运用所学知识分析问题解决问题能力,本题综合性强,难度大.
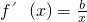 ,g'(x)=2ax-1.
,g'(x)=2ax-1.∵曲线f(x)与g(x)在公共点A(1,0)处有相同的切线,
∴
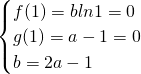 ,解得,
,解得,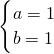 .
. (2)设P(x0,y0),则由题设有
 …①,
…①,又在点P有共同的切线,∴
 ,
,代入①得
 ,
,设
 ,则
,则 ,则h′(x)>0,
,则h′(x)>0,∴h(x)在(0,+∞)上单调递增,所以 h(x)=0最多只有1个实根,
从而,结合(1)可知,满足题设的点P只能是P(1,0).
(3)当a>0,b=1时,f(x)=lnx,
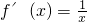 ,
,曲线f(x)在点(t,lnt)处的切线方程为
 ,即
,即 .
.由
 ,得
,得  .
.∵曲线f(x)与g(x)总存在公切线,∴关于t(t>0)的方程
 ,
,即
 (*)总有解.
(*)总有解. 若t>e,则1-lnt<0,而
 ,显然(*)不成立,所以 0<t<e,
,显然(*)不成立,所以 0<t<e,从而,方程(*)可化为
 .
.令
 (0<t<e),则
(0<t<e),则 .
.∴当0<t<1时,h'(t)<0;当1<t<e时,h'(t)>0,即 h(t)在(0,1)上单调递减,在(1,e)上单调递增.
∴h(t)在(0,e)上的最小值为h(1)=4,
所以,要使方程(*)有解,只须4a≥4,即a≥1.
所以正实数a的最小值为1.
分析:(1)因为曲线f(x)与g(x)在公共点A(1,0)处有相同的切线,所以
 ,解出即可;
,解出即可;(2)设P(x0,y0),由题设得f(x0)=g(x0),f′(x0)=g(x0),转化为关于x0的方程只有一解,进而构造函数转化为函数只有一个零点,利用导数即可证明;
(3)设曲线f(x)在点(t,lnt)处的切线方程为
 ,则只需使该切线与g(x)相切即可,也即方程组
,则只需使该切线与g(x)相切即可,也即方程组 只有一解即可,所以消y后△=0,问题转化关于t的方程总有解,分情况借助导数进行讨论即可求得a值;
只有一解即可,所以消y后△=0,问题转化关于t的方程总有解,分情况借助导数进行讨论即可求得a值;点评:本题考查利用导数研究曲线上某点切线方程问题,考查学生综合运用所学知识分析问题解决问题能力,本题综合性强,难度大.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目